- Главная
- Для учителя »
- Архив заданий олимпиад по физике за 2009-2015 годы
- Владимир Анатольевич Зверев предлагает
- Несколько ссылок на работы Анатолия Шперха
- Общие вопросы методики обучения физике
- Статьи Александра Борисовича Рыбакова »
- Важнейший общефизический принцип остается непонятым
- Рыбаков А. Б. Почитаем «Физику» вместе
- Рыбаков А.Б. Несколько замечаний о «Физике (ПС)», №10, 2015
- Рыбаков А.Б. О №12 «Физики (ПС)» и динамике автомобиля, или Спасут ли школу вузовские преподаватели?
- А.Б.Рыбаков Банджи-джампинг, сохранение импульса и уравнение Мещерского
- Рыбаков А.Б. О вращении Земли и всяком таком, или Удивительная физика в журнале «Физика (ПС)», №2/2015
- Рыбаков А.Б. Заметки о демоверсии-2012
- Экзамены »
- Конспекты »
- История физики »
- Хронология физики
- Физики. Краткие биографии
- Дополнения к биографиям
- Нобелевские премии по физике
- История методики обучения физике
- Календарь на текущий год »
- Физический календарь на 2025 год
- Календарь памятных дат в физике на 2023 год
- Юбилейные и памятные даты из истории физики в 2022 году
- Физический календарь на 2015 год
- Физический календарь на 2016 год. ч. 1
- Физический календарь на 2016 год. ч. 2
- Календарь памятных дат в физике на 2019 год
- Важнейшие юбилейные и памятные даты из истории физики в 2011 г.
- Физики в Петербурге-Петрограде-Ленинграде »
- Здесь жили и работали физики. Санкт-Петербург и Ленинградская область
- Здесь жили и работали физики. Санкт-Петербург. Адмиралтейский район
- Здесь жили и работали физики. Санкт-Петербург. Василеостровский район
- Здесь жили и работали физики. Санкт-Петербург. Петроградский район
- Здесь жили и работали физики. Санкт-Петербург. Выборгский и Калининский районы район
- Здесь жили и работали физики. Санкт-Петербург. Запад-Юг-Восток
- Здесь жили и работали физики. Санкт-Петербург. Приморский и Курортный районы
- Здесь жили и работали физики. Санкт-Петербург. Центральный район
- Библиотека »
- Медиатека »
- О нас »
Потенциальная энергия.
| Потенциальная энергия. | |
|
Потенциальная энергия - энергия взаимодействия тел или частей тела.Потенциальная энергия (от латинского potentia - возможность) определяется взаимным расположением тел или частей тела, т.е. расстояниями между ними. |
|
|
Потенциальная энергия тела, поднятого над Землей. Работа силы тяжести. |
|
|
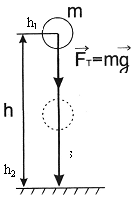
Пусть тело свободно падает с высоты h1 над уровнем Земли на уровень h2. При падении сила тяжести совершает положительную работу, при движении тела вверх - отрицательную. Величину Eз = mgh называют потенциальной энергией взаимодействия тела и Земли. |
|
|
Т.о. A = - (Ep2 - Ep1) = -ΔEp Работа сила тяжести равна изменению потенциальной энергии, взятому с противоположным знаком. Т.е., если потенциальная энергия увеличивается (тело поднимается), то сила тяжести совершает отрицательную работу и наоборот. |
Eз = mgh
A = - (Ep2 - Ep1) = -ΔEp |
|
Т.к. потенциальная энергия определяется координатой, то величина потенциальной энергии определяется выбором системы координат (выбором нулевого уровня). Т.е. она определяется с точностью до постоянной величины. В данной задаче удобно за точку отсчета выбирать уровень Земли. |
|
|
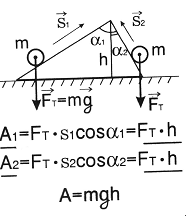
Если тело движется под углом к направлению вектора силы тяжести, то, как видно из рисунка, работа силы тяжести независимо от траектории определяется изменением положения тела (на рис. - высотой наклонной плоскости h). Если тело движется по произвольной траектории, то ее можно представить в виде суммы горизонтальных участков, на которых работа силы тяжести равна нулю, и вертикальных, на которых суммарная работа будет равна А=mgh. Работа силы тяжести не зависит от формы траектории и определяется только начальным и конечным положением тела. На замкнутой траектории работа силы тяжести равна нулю, т.к. потенциальная энергия не меняется. |
|
|
Потенциальная энергия тел, взаимодействующих посредством гравитационных сил. |
|
|
Знак "-" говорит о том, что это энергия притягивающихся тел. При сближении тел потенциальная энергия увеличивается по модулю. Работа по сближению двух астрономических объектов: |
|
|
Потенциальная энергия упруго деформированного тела. Работа силы упругости. |
|
|
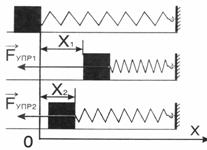
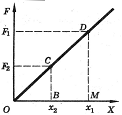
Для вывода формулы используем, что работа численной равна площади под графиком зависимости силы от координаты. При малых упругих деформациях сила упругости прямо пропорциональна абсолютной деформации (з-н Гука) - см. рис. Тогда работа при изменении деформации от х1 до х2 равна:
|
|
|
Учитывая з-н Гука, получим: |
|
|
Т.о., если принять за потенциальную энергию упруго деформированного тела величину
где k - коэффициент жесткости, а х - абсолютная деформация тела, то можно сделать вывод , что т.е. работа силы при деформации тела равна изменению потенциальной энергии этого тела, взятой с обратным знаком. |
|
|
Работа силы упругости зависит только от координат (начальной и конечной деформаций) тела и, следовательно, не зависит от траектории. Работа по замкнутой траектории равна нулю. |
|
|
Консервативные силы. Консервативными (сохраняющими) наз. силы, работа которых не зависит от траектории и по замкнутой траектории равна нулю (эти силы не зависят от скоростей). Примеры: гравитационные, упругие. |
|
|
Диссипативные силы Диссипативными (рассеивающими) наз. силы, работа которых зависит от траектории и по замкнутой траектории не равна нулю (такие силы зависят от скорости). Пример: сила трения. |
|

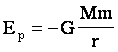 , где r- расстояние между взаимодействующими телами.
, где r- расстояние между взаимодействующими телами.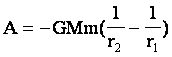 .
.
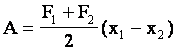 .
.
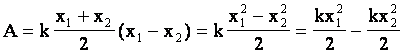
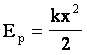 ,
,