- Главная
- Для учителя
- Архив заданий олимпиад по физике за 2009-2015 годы
- Владимир Анатольевич Зверев предлагает
- Несколько ссылок на работы Анатолия Шперха
- Общие вопросы методики обучения физике
- Статьи Александра Борисовича Рыбакова
- Важнейший общефизический принцип остается непонятым
- Рыбаков А. Б. Почитаем «Физику» вместе
- Рыбаков А.Б. Несколько замечаний о «Физике (ПС)», №10, 2015
- Рыбаков А.Б. О №12 «Физики (ПС)» и динамике автомобиля, или Спасут ли школу вузовские преподаватели?
- А.Б.Рыбаков Банджи-джампинг, сохранение импульса и уравнение Мещерского
- Рыбаков А.Б. О вращении Земли и всяком таком, или Удивительная физика в журнале «Физика (ПС)», №2/2015
- Экзамены
- Конспекты
- История физики
- Хронология физики
- Физики. Краткие биографии
- Дополнения к биографиям
- Нобелевские премии по физике
- История методики обучения физике
- Календарь на текущий год
- Физический календарь на 2026 год
- Физический календарь на 2025 год
- Календарь памятных дат в физике на 2023 год
- Юбилейные и памятные даты из истории физики в 2022 году
- Физический календарь на 2015 год
- Физический календарь на 2016 год. ч. 1
- Физический календарь на 2016 год. ч. 2
- Календарь памятных дат в физике на 2019 год
- Физики в Петербурге-Петрограде-Ленинграде
- Библиотека
- Медиатека
- О нас
Математический маятник
|
Колебания математического маятника. |
|
|
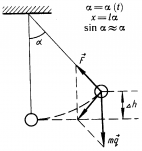
Математический маятник – материальная точка, подвешенная на невесомой нерастяжимой нити (физическая модель). |
|
|
Будем рассматривать движение маятника при условии, что угол отклонения мал, тогда, если измерять угол в радианах, справедливо утверждение: |
|
|
На тело действуют сила тяжести и сила натяжения нити. Равнодействующая этих сил имеет две составляющие: тангенциальную, меняющую ускорение по величине, и нормальную, меняющую ускорение по направлению (центростремительное ускорение, тело движется по дуге). |
|
|
Т.к. угол мал, то тангенциальная составляющая равна проекции силы тяжести на касательную к траектории: |
|
|
Сравним полученное уравнение с уравнением колебательного движения Видно, что |
|
|
Период колебаний |
Формула Галилея |
|
Важнейший вывод: период колебаний математического маятника не зависит от массы тела! |
|
|
Аналогичные вычисления можно проделать с помощью закона сохранения энергии. Учтем, что потенциальная энергия тела в поле тяготения равна |
|
|
Запишем закон сохранения энергии и возьмем производную от левой и правой частей уравнения: Т.к. производная от постоянной величины равна нулю, то Производная суммы равна сумме производных: |
|
|
Следовательно: |
|

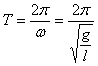 или
или  (формула Галилея).
(формула Галилея).