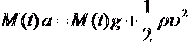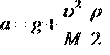А.Б.Рыбаков Банджи-джампинг, сохранение импульса и уравнение Мещерского

Очень редко появляются совсем новые сюжеты задач механики. Но сейчас такое произошло. Движение прыгуна в экстремальном аттракционе банджи-джампинг обладает некоторыми удивительными особенностями, которые требуют объяснения. Оказалось, что эти особенности легко объяснить, если применить к прыгуну и привязанному к нему канату уравнение, выведенное нашим соотечественником еще в позапрошлом веке.

Джампинг? Джампинг!

В телевизионных репортажах из дальних стран иногда промелькнет такое экстремальное развлечение: к человеку привязывают свободной конец упругого каната, другой конец которого закреплен, после чего человека сталкивают с большой высоты. Этот аттракцион называется банджи-джампинг. Много ссылок на этот аттракцион дает Интернет, попал он уже и в Википедию. Будем здесь для прост

оты называть его просто джампингом. В этом прыжке много разных фаз и соответственно много удовольствий поджидает прыгуна. Но нас сейчас интересует только одно обстоятельство – видеосъемка показала, что человек летит вниз с ускорением, превышающем g. На первый взгляд это обстоятельство представляется удивительным, ведь, казалось бы, прыгун и часть каната ускоряются только силой тяжести, никаких других сил обнаружить не удается.

Начнем с самого начала. К какому типу систем надо отнести прыгуна с канатом? Какие законы (уравнения) надо использовать для описания динамики такой системы?

Прыгун и движущаяся часть каната – это типичный пример тела с переменной массой. Во избежание недоразумений надо сказать, речь идет об изменении массы тела за счет отсоединения какой-то части вещества, составляющего тело (или присоединения вещества извне). В нашем случае при движении непрерывно увеличивается покоящаяся часть каната и, соответственно, уменьшается масса движущейся части. Это-то очевидное обстоятельств и окажется важнейшим для дальнейших рассуждений.

Поставим самые напрашивающиеся вопросы. Что происходит с импульсом системы? Что происходит с механической энергией? Как записывается основное уравнение динамики для такой системы? Попытаемся ответить на все эти вопросы.

Начнем с совсем простого, но очень важного для наших рассуждений, примера.

Щелканье кнута и закон сохранения импульса

В раннем-раннем детстве я видел в дачном поселке под Ленинградом, как местные жители встречали вечерами стадо коров (позднее коров в дачной местности уже не было). Пастух щелкал кнутом, подгоняя скотину. Вот оно!

Молодому читателю, возможно, уже надо напомнить, как устроен кнут. А устроен он очень просто: к палке (рукоятке, кнутовищу) привязан узкий длинный ремень (иногда – веревка). Это же «устройство», впрочем, называют и бичом (так в известнейшем стихотворении Некрасова эти слова стоят рядом: «Там били женщину кнутом…», «…лишь бич свистал играя»).

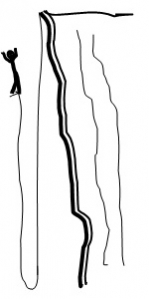
Двинув кнутовище, пастух сообщает всему ремню импульс – а дальше начинается самое для нас интересное. Конец ремня, привязанный к остановившемуся кнутовищу, тормозится, и все меньшая часть ремня продолжает движение. Но в точке перегиба никакая сила на движущуюся часть ремня не действует, значит, её импульс не уменьшается. А поскольку масса этой части ремня уменьшается, то скорость её должна увеличиваться. Итак, движущаяся часть ремня непрерывно ускоряется (см.рис.). По-видимому, конец ремня даже переходит через звук – и раздается характерный очень громкий щелчок.

Человек, привыкший к рассуждениям, основанным на втором законе Ньютона, может спросить: «Какая же сила ускоряет часть кнута?». В том-то и дело, что никакие внешние силы к ускорению части кнута не имеют отношения. Повторим: движущаяся часть ремня непрерывно ускоряется, потому что этого требует закон сохранения импульса.

Аналогия с движением каната в джампинге совершенно очевидна. Привяжите к концу ремня какое-нибудь тело – аналогия с джампингом станет еще очевиднее (а скорость конца ремня уменьшится). Но в джампинге в дело вмешивается еще и сила тяжести.

Значит, в общем случае нам надо иметь уравнение, описывающее движение тела переменной массы под действием внешних сил. В одном крайнем случае (в отсутствии внешних сил) уравнение должно обеспечивать сохранение импульса, как в случае с кнутом, в другом (при неизменной массе) – переходить в обычный второй закон Ньютона.

Порядок в этом вопросе навел еще в позапрошлом веке наш российский ученый Иван Всеволодович Мещерский.

И.В.Мещерский

Иван Всеволодович Мещерский родился в Архангельске в 1859 г. В 1878-1882 гг. учился на физико-математическом факультете Петербургского университета. После окончания университета был оставлен на кафедре. Первые результаты по интересующей нас теме относятся к 1893 г. В 1897 г. Мещерский защищает магистерскую диссертацию «Динамика точки переменной массы». Некоторые дополнительные результаты были опубликованы в 1904 г.

Эти работы Мещерского были переизданы в 1949 г. в серии «Классики естествознания» [1]. Именно это издание лежит сейчас передо мной (иногда я приносил эту книгу в класс, чтобы показать ученикам, как удручающе громоздки уравнения механики, если они записаны без использования векторных обозначений). Мещерский оставил след не только как ученый, но и как выдающийся педагог высшей школы. С 1902 г. до конца своих дней он возглавлял кафедру теоретической механики в Петербургском политехническом институте. Удивительна судьба выпущенного им в 1914 г. задачника по теоретической механике.

У меня на полке стоит 33-е издание этого задачника, увидевшее свет в 1973 г. Т.е., 33 издания были выпущены менее чем за 60 лет! Другого такого примера я не знаю. А ведь в 1973 г. история задачника отнюдь не закончилась.

Многие сюжеты, которые нам сейчас известны по школьным и вузовским задачникам, впервые появились именно в задачнике Мещерского.

Читатель, заинтересовавшийся историей этого раздела механике найдет немало интересного в статье [2].

Уравнение Мещерского

Кратко напомним основные моменты. Согласно Мещерскому основной закон динамики тела переменной массы записывается в виде:

 ,  (1)

где – сумма всех внешних сил, действующих на тело, М(t) – зависящая от времени масса системы,  – скорость изменения этой массы, – относительная скорость отсоединяемого вещества (т.е. скорость отсоединяемых частей относительно «материнского» тела). Если речь идет именно об уменьшении массы, то, конечно,  «Главный» (для всех учебников) пример применения уравнения (1) – это анализ движения ракеты, в этом примере u – скорость истечения продуктов сгорания топлива,  – массовый расход топлива.

В русскоязычной литературе уравнение (1) называют уравнением Мещерского. Оно является следствием фундаментального закона изменения импульса для системы материальных точек. Поэтому, в частности, некоторые задачи на интересующие нас тему были решены до работ Мещерского авторами, не использующими уравнение (1) (см. ниже).

Можно переписать (1) еще в таком «почти симметричном» виде:

 (2)

где, как обычно, производные по времени обозначены точками над обозначениями физической величины.

Уравнение (1) является обобщением второго закона Ньютона – к известным нам членам добавляется еще одно слагаемое. Конечно, все члены в (1) имеют размерность силы, и возникает соблазн назвать новое слагаемое тоже какой-нибудь «силой». Так обычно и поступают авторы, пишущие об уравнении Мещерского. Они называют новое слагаемое «реактивной силой». Необходимость введение такой терминологии представляется весьма сомнительной. Эти авторы просто хотят сохранить возможность говорить, что тело (даже тело переменной массы) ускоряется какой-то силой. Но это не так! И мы это уже видели на примере кнута (и еще увидим ниже – см. последний раздел статьи).

В общем случае, конечно, уравнение Мещерского является, как и второй закон Ньютона, дифференциальным уравнением второго порядка относительно функции  Ограничиваясь в школьном курсе постоянными силами (и, соответственно, равноускоренным движением), мы как бы не замечаем этих математических проблем. Но с уравнением Мещерского так поступить не удастся, кроме редчайших исключений. Практически любая содержательная задача о движении тела переменной массы приводит к дифференциальному уравнению.

Задача Кейли (A.Cayley)

Хотя бы на одном простом примере покажем, как записывается уравнение Мещерского для конкретного движения объекта интересующего нас типа и как можно, не гонясь за математической строгостью, найти его решение. Читатели, интересующиеся лишь основной линией наших рассуждений (о джампинге), вполне могут пропустить этот раздел.

В своей диссертации, в обзоре литературы Мещерский пишет: «Изменение массы, совершающееся непрерывно, рассматривает впервые, насколько мне известно, Кейли». Этот английский математик в 1857 г. опубликовал статью, в которой проанализировал следующую задачу.

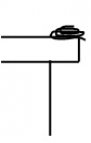Задача. Тяжелая цепь свернута в клубок на самом краю стола. Одно звено свешивается за край стола. Как будет двигаться конец цепи?

Решение. Кейли, конечно, не знал уравнения (1). Мы же будем исходить из этого уравнения. Будем отсчитывать координату конца цепи х по вертикали вниз от края стола. Запишем уравнение (1) для движущегося участка цепи длиной х. Пусть масса единицы длины цепи ρ. Тогда масса движущегося участка m = ρx, на него действует сила тяжести ρgx, за 1с масса этого участка увеличивается на ρx. Скорость элемента цепи, лежащего на столе, относительно движущегося участка цепи u_x=–υ. Так что проекция уравнения (1) на ось х примет вид:

(3)

и окончательно мы имеем следующее уравнение для функции x(t):

 (4)

Это, как уже сказано, дифференциальное уравнение второго порядка (звучит пугающе). Математики умеют решать такие уравнения, выполняя формальные преобразования, придумывая замены переменных и всякое такое. Но мы же физики – мы пойдем своим путем!

Подумаем, какого типа движение может совершать этот участок цепи? О равномерном не может быть и речи. Может быть – равноускоренное? А что? Попробуем!

Предположим, что этот участок цепи движется с неким, неизвестным нам пока постоянным ускорением . Это предположение может показаться слишком смелым, но ведь мы ничем не рискуем – если оно неправильно, мы придем к противоречию и тогда будем придумывать что-нибудь другое.

Итак, пусть

 (5)

т.е.  (6)

Подставим эти соотношения в (4) и после совсем простых алгебраических преобразований получим . Ура!

Итак, наше предположение блестяще подтвердилось – конец цепи движется с постоянным ускорением, и мы решили задачу Кейли. Если математик скривится, увидев такое «решение», объясните ему, что физик имеет право добывать информацию любым способом.

Почему сила тяжести сообщает нашей цепи ускорение меньшее g? На очень наивном языке можно было бы ответить, что часть силы тяжести тратится на приведение в движение покоящихся до этого элементов цепи. А теперь попробуйте догадаться, как будет двигаться цепь (или канат) под действием силы тяжести, если, наоборот, элементы цепи останавливаются.

Складываем коврик

А что происходит с механической энергией при движении по канату (или какому-то другому виду гибкой связи) «точки перегиба»? На первый взгляд кажется, что канат можно считать идеальным в том смысле, что при таком движении потери механической энергии не происходит. Но это не так! Рассмотрим столь простое движение интересующего нас объекта, что уравнение Мещерского сведется к алгебраическому уравнению. Эта задача есть, например, в сборнике [3] (авторы об уравнении Мещерского не упоминают).

Задача. Узкий длинный ковер (ковровая дорожка) лежит на полу. Конец ковра загибают и тянут назад со скоростью υ. Масса единицы длины ковра ρ. Какую силу F прикладывают к концу ковра?

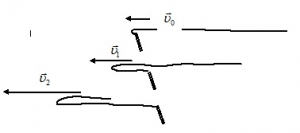
Решение. Когда конец ковра, к которому приложена сила, пройдет путь L, точка перегиба ковра пройдет путь L/2 (см.рис.), т.е. она движется не со скоростью υ, а со скоростью w=υ/2. За время Δt в движение вовлекается участок ковра длиной Δℓ=wΔt, его масса Δm=wρΔt.

Поэтому уравнение Мещерского (1) принимает совсем простой вид:

  (7)

Итак, нам известны все параметры, описывающие движение ковра. Рассмотрим разные члены в балансе энергии в тот момент, когда ковер сложен вдвое. К этому моменту точка приложения внешней силы F пройдет, как уже сказано, путь L. Значит, при этом силой F будет совершена работа

 (8)

Теперь сосчитаем кинетическую энергию движущейся части (т.е. половины) ковра:

 (9)

Мы получили, что ровно половина работы внешней силы потеряна. Такой вот удивительный результат! И нам надо запомнить на будущее, что массивные гибкие связи нельзя считать идеальными, при движении точки перегиба мы обязательно теряем заметную часть механической энергии. Но, подчеркнем, речь идет именно о массивных связях – к «невесомым» нитям, связывающим грузы в наших школьных задачах, всё это не имеет отношения.

А читатель может вспомнить, что удивительная «двойка» в балансе энергии появляется в нашем курсе в самых неожиданных местах: при зарядки конденсатора, при поднятия жидкости в капилляре и т.д.

Вернемся к джампингу

Мы подробно обсудили разные аспекты проблемы, теперь у нас все готово, чтобы выписать уравнение Мещерского для движущейся части каната и прыгуна. Направим ось х вниз, спроектируем уравнение (1) на эту ось. Будем аккуратны со знаками, вектор относительной скорости останавливающихся частей направлен вверх, поэтому u_x = –υ. Выше (в задаче о ковре) мы уже выяснили, что за единицу времени останавливается часть каната с массой , поэтому уравнение примет вид

  (10)

(M – масса движущейся части каната и самого прыгуна, t - время полета).

Перепишем (10) в виде

   (11)

Это, конечно, не решение задачи, ведь и М, и υ – неизвестные нам пока функции времени. Но, ясно, что скорость υ со временем растет, а масса М – падает. Итак, мы доказали, что ускорение прыгуна в любой момент времени больше g и растет со временем. И качественно картина явления представляется нам вполне ясной: тело с уменьшающейся массой приобретает под действием силы тяжести всё больший импульс, а, значит – ускоряется! И этот эффект будет тем сильнее, чем больше масса каната (по сравнению с массой прыгуна).

Новый опыт

Снова вернемся к понятию «реактивной силы». В элементарных курсах реактивную силу, приводящую в движение ракету, обычно объясняют, как силу давления продуктов сгорания топлива на стенку камеры сгорания. Представляется, что иногда такое «объяснение» может затемнять суть дела.

Рассмотрим совсем простой, «школьный» опыт. В кузове игрушечного автомобиля поместим длинную тяжелую ленту. Она должна быть свернута таким образом, чтобы иметь возможность покидать кузов с минимальным трением. Закрепляем конец ленты так, что она разматывалась при движении автомобиля, и толкаем автомобиль. Лента, покидая кузов и останавливаясь, не уносит импульс и, следовательно, импульс автомобиля с остатком ленты не меняется. Но масса-то уменьшилась! Значит, скорость должна увеличиться. Итак, лента разматывается – а автомобильчик разгоняется!

Ясно, что никакой «реактивной силы», толкающей автомобильчик вперед, обнаружить не удается (нет никакого давления на стенку кузова).

«Но это же то же самое, что кнут!» – может сказать читатель. Ну да! Тем удивительнее, что никакого упоминания о таком опыте я никогда не видел.

Удастся ли реально демонстрировать этот опыт ученикам, зависит от того, удастся ли экспериментатору уменьшить силу трения до необходимых значений. Указание экспериментатору: при сматывании ленты не должна меняться её высота над столом. Автомобильчик должен быть легким (по сравнению с лентой).

Автор будет благодарен всем коллегам, сообщившим о попытках проведения этого опыта.

Литература

1. Мещерский, И.В. Работы по механике тел переменной массы. М., Л., ГИТТЛ, 1949.

2. Тюлина, И.А. Два подхода к построению модели тела переменной массы. / Исследования  по истории механики. М.: Наука, 1981.

3. Гнедиг П., Хоньек Д., Райли К. Двести интригующих физических задач. М.: 2005.