- Главная
- Для учителя
- Архив заданий олимпиад по физике за 2009-2015 годы
- Владимир Анатольевич Зверев предлагает
- Несколько ссылок на работы Анатолия Шперха
- Общие вопросы методики обучения физике
- Статьи Александра Борисовича Рыбакова
- Важнейший общефизический принцип остается непонятым
- Рыбаков А. Б. Почитаем «Физику» вместе
- Рыбаков А.Б. Несколько замечаний о «Физике (ПС)», №10, 2015
- Рыбаков А.Б. О №12 «Физики (ПС)» и динамике автомобиля, или Спасут ли школу вузовские преподаватели?
- А.Б.Рыбаков Банджи-джампинг, сохранение импульса и уравнение Мещерского
- Рыбаков А.Б. О вращении Земли и всяком таком, или Удивительная физика в журнале «Физика (ПС)», №2/2015
- Экзамены
- Конспекты
- История физики
- Хронология физики
- Физики. Краткие биографии
- Дополнения к биографиям
- Нобелевские премии по физике
- История методики обучения физике
- Календарь на текущий год
- Физический календарь на 2026 год
- Физический календарь на 2025 год
- Календарь памятных дат в физике на 2023 год
- Юбилейные и памятные даты из истории физики в 2022 году
- Физический календарь на 2015 год
- Физический календарь на 2016 год. ч. 1
- Физический календарь на 2016 год. ч. 2
- Календарь памятных дат в физике на 2019 год
- Физики в Петербурге-Петрограде-Ленинграде
- Библиотека
- Медиатека
- О нас
Рыбаков А.Б. Несколько замечаний о «Физике (ПС)», №10, 2015
©Рыбаков А.Б.
Несколько замечаний о «Физике (ПС)», №10, 2015
«И снова – о законе Архимеда»
Так называется опубликованная в журнале статья, посвященная анализу двух задач. В обеих задачах речь идет об одинаковых стаканах с одинаковыми объе-мами воды в них. В эти стаканы авторы будут помещать два шарика одинакового объёма, но разной массы.
Скажем прямо, решения авторов вызывают оторопь! Наверно, авторы никогда не решали школьные задачи.
1.
В условии первой задачи легкий шарик плавает в толще воды, прикрепленный нитью ко дну первого стакана. А во второй стакан опускают на нити тяжелый шарик и держат его так, чтобы он не касался дна. Какой из стаканов тяжелее?
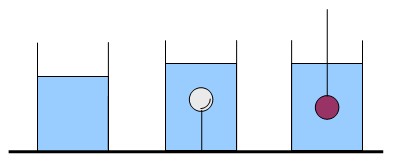
Задача, по-моему, решается в один шаг. Заметьте, что предлагаемое мною решение короче условия!
Высота столба воды в стаканах одинакова, следовательно, одинакова и сила давления воды на дно, но в первом стакана нить тянет дно наверх, следовательно, первый стакан легче. Вот и всё!
А можно рассуждать и иначе. Пусть нить в первом стакане развязалась. Из-за этого вес содержимого стака-на измениться не может. Легкий шарик всплывет, высота столба воды уменьшится. Ответ стал еще очевиднее.
2.
Но еще «интереснее» вторая задача. Здесь в левый стакан кладут легкий шарик, а в правый – более тяжелый. И авторы спрашивают, какой стакан тяжелее?
По сути дела, в задаче спрашивается, какой шарик тяжелее – легкий или тяжёлый.
Так что никакой задачи просто нет!
Но авторы, по-видимому, этого не понимают.
«Но вы же не сказали, что в нашей задаче тяжелый шарик плавает в толще воды!» – могут возмутиться они. Потому и не сказал, что это условие ни к чему. Плавает ли он в толще, всплыл ли на поверхность, лежит ли на дне – все это никак не влияет на решение задачи! Во всех случаях он вносит в вес стакана свой вес.
Авторы не понимают аддитивности массы. Не понимают, что масса системы «стакан+вода+шарик» не зависит от конфигурации системы. Вес системы не зависит от природы и свойств внутренних сил.
Так что разбираться в многословных рассуждениях авторов нет никакого смысла. А вообще-то, качественные задачи на плавание тел очень интересны. По мере сил я пытался показать это в своей статье «Качественные задачи на силу Архимеда» («Потенциал», №8, 2014).
Вес и всякое такое
В «Учительских заметках» Дружинина Б.Л. обсуждается вопрос о том, что такое вес.
Заметки сопровождает рисунок от руки. Отсутствие стрелочек над обозначе-ниями векторов в учебном журнале бросается в глаза. Меня так и тянет расста-вить на этом рисунке стрелочки, но не будем отвлекаться. Далее ученик говорит: «Когда на карусели катаешься, то … вес состоит из векторной суммы mg и Fц» (где Fц – центробежная сила). И учитель (т.е. автор) никак не комментирует это высказывание. Наверно, согласен с ним.
А я прокомментирую.
Вопрос о реальности центробежной силы (и, вообще, сил инерции) довольно сложен. Можно ли, стоит ли говорить об этой силе походя, между делом? Ведь молодые коллеги могут понести это на урок. А любой разговор о центробежной силе неизбежно обнаружит противоречие с фундаментальным (школьным!) опре-делением силы, как меры взаимодействия тел! Ну, хорошо, допустим, что ученики автора в этом вопросе досконально разобрались.
Теперь о весе.
На рисунке автора хорошо видно, что вес Р приложен к телу человека, а это, конечно, не так.
Теперь о том, стоит ли называть весом силу, направленную вбок?
Учитель обязан использовать термины строго в том смысле, как это принято в сообществе. А этот смысл зафиксирован в «главных» справочниках и наиболее авторитетных учебниках и монографиях. У учителя нет права на оригинальную трактовку термина.
А то понимание термина «вес», которое выражено в тексте и на рисунке, не находит подтверждения ни в самом авторитетном физическом справочнике (Физический энциклопедический словарь, 1983, гл.ред. акад. Прохоров А.М.), ни в серьёзных учебниках.
Один из лучших курсов общей физики (Сивухин Д.В.) пишет совершенно определенно: «Когда говорят о весе тела, обычно предполагают, что тело, подставка и подвес покоятся относительно Земли».
«Подумаешь, ерунда» – скажет иной читатель.
Нет! Учебные журналы и предназначены для того, чтобы в них вырабатыва-лись общие представления, чтобы от Олимпа (т.е. ФИПИ) до моего коллеги – ря-дового учителя все понимали термины одинаково.
Повторю, ни результат взвешивания на карусели, ни направленная вбок сила давления человека на сиденье карусели не называются весом.
Получив журнал и увидев этот материал Дружинина, я сразу написал автору: «На какие авторитетные источники Вы опираетесь при таком понимании термина "вес"»? Как это обычно и бывает, автор не ответил.
О спутниках
В тех же заметках после беглого обсуждения динамики спутника на круговой орбите приводится такое высказывание ученика: «Всё ясно, – говорит Саша. – Если скорость увеличить, то радиус орбиты уменьшится, и наоборот, если ско-рость уменьшить, то радиус вырастет». Я немало лет работал в Военно-космическом кадетском корпусе и за такие небрежные высказывания по нашей «самой главной» теме ставил двойки своим кадетам. Автор же никак не коммен-тирует это высказывание. И опять я с грустью думаю, что, опираясь на авторитет столичного журнала, молодой коллега понесет эти мысли на урок.
А дело обстоит совсем не так. Если в какой-то точке М круговой орбиты рыв-ком увеличить скорость спутника, то он перейдет на орбиту с большей полной энергией – на эллиптическую орбиту, для которой точка М будет перигеем. Если рывком уменьшить скорость спутника, то он перейдет на эллиптическую орбиту с меньшей энергией, для которой точка М будет апогеем (или войдет в плотные слои атмосферы).
В разговоре о спутниках опасно опираться на «очевидности». Напомню, что при торможении спутника в верхних слоях атмосферы он ускоряется!
Подробно о движении спутников я писал в пособии «Основы теории движе-ния космических аппаратов (методическое пособие для учащихся 10,11-х классов». СПб., ВККК, 2000 г.).
«Материальная точка» в кинематике?
«Дать определение скорости материальной точки» просят авторы из МГУ своих абитуриентов и читателей журнала (стр.53).
Надо прямо сказать, что ни определения, ни уравнения кинематики не зависят от того, о материальном объекте идет речь или нет. Все авторы классических учебников механики хорошо это понимали. В кинематике у них есть тема «Движение точки», в динамике у них есть тема «Уравнения движения материальной точки».
Но ведь ошибки в вопросе авторов из МГУ нет?
Ошибки нет. Есть отсечение большого класса интереснейших объектов.
А разве бывают нематериальные объекты?
Сколько угодно. Например, бегущая по земле тень от летящего самолета. Или зайчик от прожектора на далеком экране. Зайчик, конечно, светится, потому что на экран в этом месте попали фотоны, но он не «состоит из фотонов», эти фотоны не перемещаются вместе с зайчиком. На такие объекты не распространяется ограничение, накладываемое СТО – скорость таких объектов может превышать скорость света. Я уже писал об этом в статье «Заметки об изучении кинематики», «Физика (ПС)», 2009, №11.
Но есть и объекты еще более хитрой природы. (Интересующихся отсылаю к своей статье «Распространение сигнала от движущегося источника, или Что уви-дит наблюдатель?», «Квант», 2013, №4). Так вот, определение скорости должно быть пригодно для объектов всех типов.
А разве бывают нематериальные объекты?
Сколько угодно. Например, бегущая по земле тень от летящего самолета. Или зайчик от прожектора на далеком экране. Зайчик, конечно, светится, потому что на экран в этом месте попали фотоны, но он не «состоит из фотонов», эти фотоны не перемещаются вместе с зайчиком. На такие объекты не распространяется ограничение, накладываемое СТО – скорость таких объектов может превышать скорость света. Я уже писал об этом в статье «Заметки об изучении кинематики», «Физика (ПС)», 2009, №11.
Но есть и объекты еще более хитрой природы. (Интересующихся отсылаю к своей статье «Распространение сигнала от движущегося источника, или Что уви-дит наблюдатель?», «Квант», 2013, №4). Так вот, определение скорости должно быть пригодно для объектов всех типов.
