Превращение энергии при гармонических колебаниях. Затухающие колебания.

Превращение энергии при гармонических колебаниях.

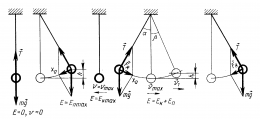
На примере колебаний тела на нити видим, что в положении равновесия скорость и, следовательно, кинетическая энергия тела максимальны. Если потенциальную энергию отсчитывать от положения равновесия, то она максимальна при амплитудном значении смещения, т.е. когда кинетическая энергия (скорость) равна нулю.

Т.к. мы рассматриваем свободные колебания (происходящие в отсутствие трения), то выполняется закон сохранения механической энергии: сумма кинетической и потенциальной энергий остается неизменной:

Пусть колебание происходит по закону синуса, тогда скорость меняется по закону косинуса. Запишем выражение для кинетической энергии: .

Согласно закону сохранения энергии, полная энергия будет равна максимальной кинетической, т.к. в положении равновесия потенциальная равна нулю. Тогда: . Для потенциальной энергии получим: 

Т.о. мы видим, что

колебания кинетической и полной энергий происходят в противофазе.

ЗАТУХАЮЩИЕ КОЛЕБАНИЯ.

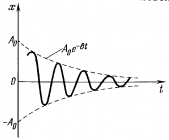
Затухающими наз. колебания, энергия (а значит, и амплитуда) которых уменьшается с течением времени. Затухание свободных механических гармонических колебаний связано с убыванием механической энергии за счет действия сил сопротивления и трения.

Если сила сопротивления пропорциональна скорости относительного движения , то амплитуда колебаний изменяется по закону, где x₀ – начальная амплитуда, - коэффициент затухания, характеризующий быстроту убывания амплитуды, e – основание натурального логарифма.

Затухающие колебания не являются истинно периодическим процессом, т.к. в них никогда не повторяются значения физических величин.

Условным периодом затухающих колебаний наз. промежуток времени между двумя состояниями колеблющейся системы, в которых физические величины, характеризующие колебания, принимают аналогичные значения, изменяясь в одном и том же направлении: ,

где ω₀ – собственная частота свободных колебаний.

Мы видим, что период затухающих колебаний больше, чем период незатухающих колебаний с теми же параметрами колебательной системы.

При условии δ < ω₀ затухающие колебания описываются уравнением , где  .

Если δ > ω₀, то трение в системе очень велико и колебаний не происходит, запас механической энергии тела к моменту его возвращения в положение равновесия полностью расходуется на преодоление трения.
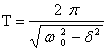