Рыбаков А.Б. Заметки о демоверсии-2012

Цель этих заметок – указать на некоторые неточности в условиях или решениях демоверсии-2012.

1. Задание С3

Необходимо расплавить лёд массой 0,2 кг, имеющий температуру 0ºС. Выполнима ли эта задача, если потребляемая мощность нагревательного элемента – 400 Вт, тепловые потери составляют 30%, а время работы нагревателя не должно превышать 5 минут?

Возможное решение

Согласно первому началу термодинамики количество теплоты, необходимое для плавления льда, ΔQ₁ = λm, где λ – удельная теплота плавления льда. ΔQ₂ – подведённое джоулево тепло: ΔQ₂ = ηPt. В соответствии с заданными условиями ΔQ₁ = 66 кДж и ΔQ₂ = 84 кДж, а значит, ΔQ₁ < ΔQ₂, и поставленная задача выполнима.

Критерии оценивания выполнения задания

Приведено полное решение, включающее следующие элементы:

I) записаны положения теории и физические законы, закономерности, применение которых необходимо для решения задачи выбранным способом (в данном случае I начало термодинамики, закон Джоуля – Ленца);

II) описаны все вводимые в решение буквенные обозначения физических величин (за исключением, возможно, обозначений констант, указанных в варианте КИМ и обозначений, используемых в условии задачи);

III) проведены необходимые математические преобразования (допускается вербальное указание на их проведение) и расчеты, приводящие к правильному числовому ответу (допускается решение "по частям" с промежуточными вычислениями);

IV) представлен правильный ответ с указанием единиц измерения искомой величины

Совсем простая задачка на уровне 8-го класса. Какие тут могут быть проблемы?

А проблемы возникают в авторском решении и в «Критериях оценивания».

Сначала скажем о грамотности используемых в авторском решении обозначений.

Бросается в глаза, что все обозначения количеств теплоты снабжены знаком Δ. Обычно этот знак (греческая буква «дельта») в физических текстах используется для обозначения изменения какой-то величины. Но можно ли говорить о ΔQ?

Напомним, что в записи первого начала  стоят  физические величины разной природы: внутренняя энергия U – функция состояния, а Q и A – характеристики процесса (перехода из одного состояния в другое). Можно поставить вопрос о том, чему равна внутренняя энергия в определенном состоянии, но нельзя поставить такой же вопрос о количестве теплоты или работе. Нет никакой величины Q, изменением которой являлось бы ΔQ. Так что ниже мы, цитируя авторское решение, будем все же опускать Δ.

Авторы утверждают, что в решении задачи используются первое начало термодинамики и закон Джоуля-Ленца. Но где же, в каком месте приведенного ими решения?

Соотношение Q₁=λm  утверждает лишь, что тепло, необходимое для плавления какого-то тела, пропорциональна массе тела. Это обстоятельство вполне было ясно любому вменяемому человеку задолго до открытия первого начала.

Во второй фразе некоторые неясности возникают в связи с обозначением η. Обычно при решении задачи вводят обозначения для тех величин, численные значения которых приведены в тексте задачи. Т.е. в данном случае надо было как-то обозначить величину, равную 0,3. Но авторы поступают иначе, без комментариев вводят в решение η – кпд нагревателя. Заметим, что тем самым они не выполняют требования п.III своих «критериев».

Обсудим вторую фразу: «Подведенное джоулево тепло Q₂ = Pηt». «Подведенное» – к какому телу? Ко льду? Или к нагревателю? По-видимому, ко льду. Но разве можно использовать термин «джоулево», для тепла, подводимого от нагревателя ко льду?  Наверно, именно формулу Q₂ = Pηt авторы называют «законом Джоуля-Ленца». Но приведенная формула является просто следствием определения мощности и кпд, и никакого отношения к закону Джоуля-Ленца не имеет.

Именно опасения, что абитуриентам могут снижать оценки за отсутствие указаний на неиспользуемые в решении законы, и вызвали к жизни эти заметки.

Снова вернемся к «мелочам» –  к грамотности обозначений. t  обычно в физике обозначает момент времени.  Для обозначения длительности какого-то процесса правильнее было бы использовать обозначение Δt (или τ, или Т).  Приведем пример грамотного использования обозначений: «Варианты контрольных работ были розданы учащимся в момент времени t₁=12 час 15 мин. Ученики писали контрольную работу в течение времени Δt = 40 мин».

Резюмируем. Поставить 3 балла за приведенное авторами решение нельзя – там нарушены все пункты «Критериев…».

2. Задание А23

Подвешенный на нити грузик совершает гармонические колебания. В таблице представлены координаты грузика через одинаковые промежутки времени. Какова примерно максимальная скорость грузика?

1) 1,24 м/с      2) 0,31 м/с      3) 0,62 м/с     4) 0,4 м/с

Эта задача (быть может, с другими числами) давно гуляет по пособиям ФИПИ (например, она есть в пособии «ЕГЭ-2010»).

Напомню, что координату в любой задаче можно ввести самыми разными способами. Например, и в этой задаче можно было бы в качестве координаты использовать высоту грузика. Я бы, формулируя задачу такого типа, указал бы, что координата отсчитывается вдоль траектории грузика.

Признаюсь, что, прочитав бегло текст задания, я его не понял. Сразу видно, что точки размещены следующим образом:

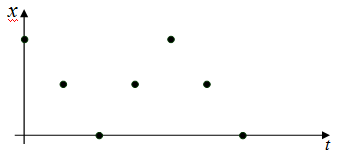
Провел «эксперименты» с несколькими коллегами и учениками. Во всех случаях видел, сколь много времени тратили «подопытные» на осознание задания. Некоторые даже говорили: «Ну, здесь же нет гармонического колебания…».

Я не говорю, что задание сформулировано некорректно. Я говорю, что экзаменующийся потратит много времени крайне непродуктивно. Стоит ли формулировать задания таким образом? Не знаю, какие цели преследовали авторы, и оставлю этот вопрос открытым. Дело ведь не только в этом. Дело в том, что таким замысловатым условием авторы обманули сами себя.

Для решения надо перейти к координате x′ = x – 2 и провести синусоиду по данным таблицы.

Обратимся к рисунку. Жирные точки на рисунке  поставлены по данным таблицы в условии. Так вот, авторы сочли, что через выделенные точки можно провести только одну синусоиду (штриховая кривая на рисунке), но через те же точки можно провести и синусоиду с частотой в 3 раза большей (сплошная кривая на рисунке) и множество других синусоид. Все такие синусоиды вполне удовлетворяют авторским условиям. И потому задача становится совершенно неопределенной.

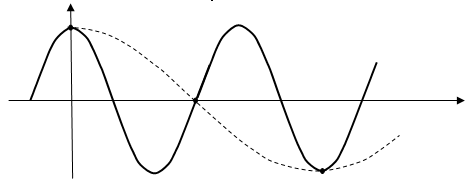
Самым простым способом исправить ситуацию было бы задание координат промежуточных точек.

3. Задание А24

У теплового двигателя, работающего по циклу Карно, температура нагревателя – 500 К, а температура холодильника – 300 К. Рабочее тело за один цикл получает от нагревателя 40 кДж теплоты. Какую работу совершает при этом рабочее тело двигателя?

1) 1,6 кДж      2) 35,2 кДж      3) 3,5 кДж       4) 16 кДж

Для использования известного выражения для кпд мало сказать, что двигатель работает по циклу Карно, надо еще указать, что он идеальный, т.е. работает без механических потерь.

Задание С6. Значение энергии пиона в решении не используется.

Порадуемся тому, что, наконец, ушел в прошлое термин «масса покоя», а с ним и «релятивистская масса».