О ПЛАВАЮЩИХ ТЕЛАХ

Книга первая

Предположим, что жидкость имеет такую природу, что из ее частиц, расположенных на одинаковом уровне и прилежащих друг к другу, менее сдавленные выталкиваются более сдавленными и что каждая из ее частиц сдавливается жидкостью, находящейся над ней по отвесу, если только жидкость не заключена в каком-нибудь сосуде и не сдавливается еще чем-нибудь другим².

I

Если поверхность, рассекаемая любой плоскостью, переходящей через одну и ту же точку, всегда дает в сечении окружность круга с центром в той самой точке, через которую проводятся секущие плоскости, то эта поверхность будет шаровой.

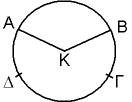Действительно, пусть будет некоторая поверхность, которая при сечении плоскостью, проходящей через точку К (рис. 1), всегда образует окружность круга с центром в этой самой точке К. Если эта поверхность не будет поверхностью шара, то не будут равными все линии, которые идут от центра к поверхности. Пусть А, В, Г, ? будут точки на поверхности, причем линии АК и ВК не будут равны; проведем через КА, КВ плоскость, и пусть она образует в сечении с поверхностью линию ?ABГ; эта линия будет, конечно, круговой с центром в точке К, так как рассматриваемая поверхность предполагалась обладающей таким свойством³. Значит, линии КА, КВ не будут неравными; поэтому необходимо, чтобы эта поверхность была шаровой.

II

Поверхность всякой жидкости, установившейся неподвижно, будет иметь форму шара, центр которого совпадает с центром Земли.

Вообразим некоторую жидкость, которая установилась неподвижно; рассечем ее поверхность через центр Земли плоскостью; пусть центр Земли будет К (рис. 2), а линия сечения поверхности АВГ?. Я утверждаю, что линия АВГ? будет окружностью круга с центром в К. Действительно, если это не так, то прямые, выходящие из К к линии АВГ?, не будут равны друг другу. В таком случае возьмем некоторую прямую, которая была бы больше одних и меньше других из линий, выходящих из К к линии АВГ?, и из центра К опишем круг радиусом, равным этой линии; тогда поверхность этого круга пойдет так, что часть ее расположится вне линии АВГ?, часть же внутри, так как радиус ее будет больше некоторых из линий, выходящих от К к линии АВГ?, и меньше других. Пусть окружность описанного круга будет ZBH; проведем из В в К прямую и построим прямые ZK, KEП, образующие равные углы [АK? и ВКП]⁴, затем из центра К опишем некоторую дугу ?OП, которая находилась бы на плоскости [чертежа] и в жидкости; тогда расположенные по дуге ?OП частицы жидкости будут находиться на одном уровне и прилегать друг к другу. Те из них, которые находятся на дуге ?O, будут сдавливаться жидкостью, расположенной до уровня ZB, а те, которые находятся на дуге ОП,-жидкостью до уровня BE; следовательно, частицы жидкости, расположенные на дугах ?O и ОП, будут сдавливаться неодинаково; таким образом, менее сдавливаемые будут вытеснены более сдавливаемыми; следовательно, жидкость не останется неподвижной. Мы же предположили, что она установилась так, что остается неподвижной; значит, необходимо, чтобы линия ABГ? была окружностью круга с центром в К. Подобным же образом докажем, что если как-нибудь иначе рассечь поверхность жидкости плоскостью, проходящей через центр Земли, то сечение будет окружностью круга и центр ее будет тот же, что и центр Земли. Теперь ясно, что поверхность установившейся неподвижно жидкости имеет форму шара с тем же центром, что и у Земли, ибо она такова, что при рассечении ее плоскостями, проходящими через одну и ту же точку, в сечении получаются окружности с центрами в той же самой точке, череа которую проходят секущие плоскости.

III

Тела, равнотяжелые с жидкостью⁴, будучи опущены в эту жидкость, погружаются так, что никакая их часть не выступает над поверхностью жидкости, и не будут двигаться вниз. <...>

IV

Тело, более легкое, чем жидкость, будучи опущено в эту жидкость, не погружается целиком, но некоторая часть его остается над поверхностью жидкости. <...>

V

Тело, более легкое, чем жидкость, будучи опущено в эту жидкость, погружается настолько, чтобы объем жидкости, соответствующий погруженной [части тела], имел вес, равный весу всего тела. <...>

VI

Тела, более легкие, чем жидкость, опущенные в эту жидкость-насильственно, будут выталкиваться вверх с силой, равной тому весу, на который жидкость, имеющая равный объем с телом будет тяжелее этого тела.

Пусть будет некоторое тело А (рис. 3), более легкое, чем жидкость; пусть В будет вес тела А, а ВН⁵Г - вес жидкости в объеме, равном А. Требуется доказать, что насильно погруженное в жидкость тело А будет выталкиваться вверх с силой, равной весу Г.

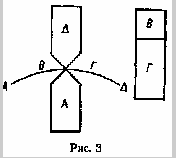Возьмем какое-нибудь тело ?, имеющее вес, равный Г; тогда тело, составленное из объединенных вместе обоих тел A, ?, будет легче жидкости [в том же объеме], так как вес тела, составленного из обоих, будет В + Г, вес же жидкости в равном объеме будет больше, чем В + Г, так как В + Г представляет вес [жидкости] в объеме, равном А. Теперь тело, составленное из обоих тел A, ?, будучи опущено в жидкость, погрузится настолько, чтобы жидкость в объеме, равном погруженной части, имела вес, равный весу всего тела, как это доказано выше. Пусть дуга ABГ? представляет поверхность некоторой жидкости. Теперь, поскольку количество жидкости в объеме, равном телу А, имеет вес, одинаковый с весами обоих тел A, ?, то ясно, что погруженная часть этого тела будет иметь объем, равный А, остальная же часть его, именно ?, будет находиться над поверхностью жидкости; действительно, если бы это тело погрузилось иначе, то получилось бы [противоречие] с тем, что было доказано [раньше]. Теперь ясно, что [с какой силой] тело А выталкивается кверху, [с такой же силой оно будет придавливаться] книзу находящимся над ним телом ?, поскольку ни то, ни другое не пересиливают друг друга. Но ? давит вниз с тяжестью, равной весу Г, так как было предположено, что вес тела ? равен Г; теперь то, что требовалось доказать, будет очевидно.

VII

Тела, более тяжелые, чем жидкость, опущенные в эту жидкость, будут погружаться, пока не дойдут до самого низа, и в жидкости станут⁶ легче на величину веса жидкости в объеме, равном объему погруженного тела⁷.

Что тело будет погружаться, пока не дойдет до самого дна, очевидно, так как находящиеся под ним частицы жидкости будут испытывать большее давление, чем другие, расположенные на одном с ним уровне, так как тело предполагается более тяжелым, чем жидкость; а что оно, как сказано, [в жидкости] станет легче, это следует доказать.

Пусть будет некоторое тело А (рис. 4), более тяжелое, чем жидкость; пусть вес тела А будет В + Г, вес же жидкости в объеме, равном А, будет В. Требуется доказать, что тело А, находясь в жидкости, будет иметь вес, равный Г.

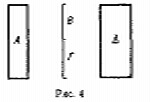Возьмем некоторое тело ?, [более легкое, чем жидкость в его объеме; пусть] вес тела ? будет равен весу В, вес же жидкости, имеющий одинаковый с ? объем, пусть будет равен весу В + + Г. Если мы сложим оба наши тела А и ? в одно, то составленное тело будет равнотяжелым с жидкостью; действительно, вес обоих этих тел равен вместе взятым весам В + Г и В, вес же жидкости, имеющей объем, равный обоим телам, равен тем же самым весам. Значит, если эти тела опустить в жидкость, то они будут в равновесии с жидкостью и не будут двигаться ни вверх, ни вниз; вследствие этого тело А пойдет вниз с такой же силой, с какой тело ? будет увлекаться вверх; тело же ?, поскольку оно легче жидкости, будет двигаться вверх с силой, равной весу Г, так как доказано, что более легкие, чем жидкость, тела, будучи насильно погружены в эту жидкость, движутся вверх с силой, равной тому весу, на который жидкость, имеющая объем, равный этому телу, будет тяжелее последнего. Но жидкость, имеющая равный объем с телом ?, будет тяжелее тела ? на вес Г; теперь ясно, что тело А будет двигаться вниз [с силой, равной весу Г].

Предположим, что все тела, движущиеся⁸ в жидкости вверх, будут подыматься по отвесной линии, проведенной через их центр тяжести.

VIII

Если какое-нибудь тело, более легкое, чем жидкость, и имеющее форму сегмента шара, будет опущено в жидкость таким образом, чтобы основание сегмента не касалось жидкости, то это тело установится в прямом положении, так что ось сегмента будет расположена по отвесу; и если кто-нибудь принудит тело стать так, чтобы основание сегмента касалось жидкости, то оно не останется в наклонном положении, но, будучи отпущено, снова станет прямо. <...>

IX

И так же если какое-нибудь тело, более легкое, чем жидкость, будет опущено в эту жидкость так, чтобы все его основание было целиком в жидкости, то тело установится в прямом положении так, что его ось расположится по отвесной линии. <...>

*В кн.: Архимед. Соч. M, 1962, с. 328-334. 
²Это модель жидкости, предлагаемая Архимедом. 
³3Именно, что все сечения ее плоскостями, проходящими через точку К, являются круговыми. (Прим. пер.) 
⁴Здесь и далее в квадратных скобках стоят добавления переводчика. 
⁵Здесь Архимед неявно вводит понятие об удельном весе как отношении; веса к объему тела. 
⁶ Характерное выражение «станут легче» .., показывающее, что греки вес одного и того же тела не считали постоянным, они «вес» понимали как «давление». (Прим. пер.) 
⁷Это и есть знаменитый закон Архимеда в его собственной формулировке. 
⁸Надо помнить, что в греческой механике идея движения была неразрывно связана с идеей силы; поэтому ближе к смыслу было бы сказать «выталкиваемые в жидкости вверх». (Прим. пер )