| Относительность механического движения. |
- Механическое движение можно наблюдать только относительно других тел. Обнаружить изменение положения тела, если не с чем сравнивать невозможно.
- В различных системах отсчета физические величины (скорость, ускорение, перемещение и т.д.), характеризующие движение одного и того же тела, могут быть различными.
- Характер движения, траектория движения и т.п. могут быть различны в разных системах отсчета для одного и того же тела могут быть различны.
|
|
|
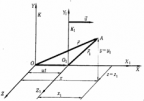
Пусть две СО движутся друг относительно друга с постоянной скоростью 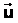 . Положение точки А в неподвижной системе К задано вектором . Положение точки А в неподвижной системе К задано вектором 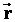 , а в движущейся системе К1 - вектором , а в движущейся системе К1 - вектором 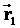 . Из чертежа видим, что . Из чертежа видим, что 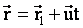 . Это уравнение позволяет переходить из одной СО в другую. . Это уравнение позволяет переходить из одной СО в другую.
При этом мы считаем, что время течет в обеих СО одинаково.
Будем условно называть системуК неподвижной, а систему К1 - движущейся. |
 |
|
Тогда для случая, когда координаты y и z не меняются, получим:
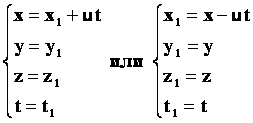 - преобразования Галилея. - преобразования Галилея.
|
|
|
Из этих уравнений следует:
- расстояние между двумя точками абсолютно, т.е. не зависит от выбора СО. Пусть в неподвижной СО координаты точек x и x', а в подвижной соответственно x1 и x1'. Тогда 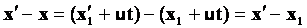 ; ; 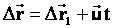
Разделим правую и левую часть уравнения на промежуток времени, в течение которого шло перемещение.
Получим: 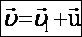
- закон сложения скоростей.Здесь скорость точки относительно неподвижной СО равна векторной сумме скорости точки относительно подвижной СО и скорости самой подвижной СО относительно неподвижной. |
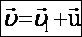 |
|
Скорость подвижной СО относительно неподвижной наз. переносной скоростью.
|
|
|
При решении задач часто бывает удобно принимать одно из движущихся относительно Земли тел за неподвижное. Тогда скорость Земли в этой СО будет равна по величине и противоположна по направлению скорости данного тела.
|
|
|
Если скорости v1 и u сонаправлены (тела сближаются), то их проекции складываются, если противоположно направлены (тела удаляются) – вычитаются.
Если скорости направлены под прямым углом - 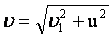 , если угол произвольный, то необходимо пользоваться теоремой косинусов: , если угол произвольный, то необходимо пользоваться теоремой косинусов: 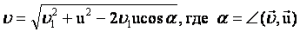 . .
|
|
|
Эти выводы справедливы для скоростей много меньших скорости света в вакууме (3.108м/с).
|
|


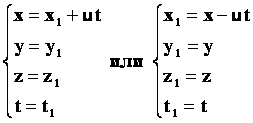 - преобразования Галилея.
- преобразования Галилея.