- Главная
- Для учителя
- Архив заданий олимпиад по физике за 2009-2015 годы
- Владимир Анатольевич Зверев предлагает
- Несколько ссылок на работы Анатолия Шперха
- Общие вопросы методики обучения физике
- Статьи Александра Борисовича Рыбакова
- Важнейший общефизический принцип остается непонятым
- Рыбаков А. Б. Почитаем «Физику» вместе
- Рыбаков А.Б. Несколько замечаний о «Физике (ПС)», №10, 2015
- Рыбаков А.Б. О №12 «Физики (ПС)» и динамике автомобиля, или Спасут ли школу вузовские преподаватели?
- А.Б.Рыбаков Банджи-джампинг, сохранение импульса и уравнение Мещерского
- Рыбаков А.Б. О вращении Земли и всяком таком, или Удивительная физика в журнале «Физика (ПС)», №2/2015
- Экзамены
- Конспекты
- История физики
- Хронология физики
- Физики. Краткие биографии
- Дополнения к биографиям
- Нобелевские премии по физике
- История методики обучения физике
- Календарь на текущий год
- Физический календарь на 2026 год
- Физический календарь на 2025 год
- Календарь памятных дат в физике на 2023 год
- Юбилейные и памятные даты из истории физики в 2022 году
- Физический календарь на 2015 год
- Физический календарь на 2016 год. ч. 1
- Физический календарь на 2016 год. ч. 2
- Календарь памятных дат в физике на 2019 год
- Физики в Петербурге-Петрограде-Ленинграде
- Библиотека
- Медиатека
- О нас
Кинематические следствия специальной теории относительности.
|
Кинематические следствия СТО Относительность одновременности |
|
|
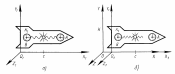
Согласно представлениям классической механики два события, происходящие одновременно в какой-либо инерциальной системе отсчета (ИСО), являются одновременными и в любой другой ИСО. Это следует из ньютоновской концепции абсолютного времени. Из второго постулата теории относительности, согласно которому скорость распространения сигналов является величиной конечной, следует, что в разных ИСО время течет по-разному. Поэтому согласно теории относительности события, являющиеся одновременными в одной ИСО, неодновременны в другой ИСО, движущейся относительно первой. Например, для наблюдателя внутри ракеты будильники А и В, срабатывающие по световому сигналу от источника, находящегося от них на одинаковом удалении, зазвонят одновременно. Для наблюдателя, относительно которого ракета движется, будильник А удаляется от точки вспышки, а будильник В - приближается. Следовательно, будильник Азазвенит позже (скорость света во всех ИСО одинакова, а до А свету надо пройти большее расстояние, чем до В). |
|
|
Относительность промежутков времени (замедление времени) Промежуток времени между двумя событиями имеет наименьшее значение в системе отсчета, связанной с движущимся объектом, где происходит исследуемое явление, которое определяется по формуле Например, если космонавты отправляются к звездной системе (и обратно), находящейся на расстоянии 500 световых лет от Земли, со скоростьюv=0,9999c, то на это потребуется по их часам 14,1 года; в то время как на Земле пройдет 10 веков. Этот результат является основой "парадокса близнецов" в СТО. Пусть один из двух близнецов решает стать космонавтом и летит на корабле со скоростьюv относительно Земли. Тогда по возвращении он окажется младше своего брата, все время остававшегося на Земле. С другой стороны, так как все ИСО равноправны, можно считать, что Земля двигалась относительно корабля с той же скоростью. Тогда помолодеть должен другой близнец. Разрешить парадокс можно, если понять, что на самом деле системы, связанные с Землей и кораблем неравноправны, т.к. корабль не все время являлся ИСО (в процессах старта, поворота, приземления он двигался с ускорением). Процессы в неинерциальных СО рассматриваются в общей теории относительности, где доказывается, что на самом деле Δ t > Δ to. Релятивистское замедление времени экспериментально подтверждено в опытах с распадом некоторых элементарных частиц (мюонов). |
|
|
Относительность длин (расстояний)
В классической механике считается очевидным, что длина стержня имеет одинаковое значение во всех ИСО. Согласно же теории относительности длина тела не является абсолютной величиной, а зависит от скорости движения тела относительно ИСО и определяется по формуле
где ℓо—собственная длина стержня; ℓ—длина этого стержня в системе отсчета K1 относительно которой стержень движется со скоростью v. Эту формулу, как и в предыдущем случае, легко получить из преобразований Лоренца, учитывая, что длина любого отрезка - это разность координат его начала и конца. Из этой формулы следует l<l0, что значит: в ИСО, движущихся друг относительно друга со скоростью, близкой к скорости света в вакууме, наблюдается релятивистский эффект сокращения длины тела. |
|
|
Релятивистский закон сложения скоростей Классический закон сложения скоростей Запишем (без доказательства) закон сложения скоростей для частного случая, когда тело А движется вдоль оси ОХ со скоростью v1 относительносистемы отсчета K1, а система отсчета K1 движется относительно системы К со скоростью v. Скорость тела А относительно системы К обозначим через и.Тогда согласно релятивистскому закону сложения скоростей
Если скорости v и v1 много меньше скорости света, то величина В любом случае выполняется условие |
|

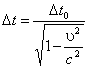 . Эту формулу легко получить из преобразований Лоренца, учитывая, что Δt=t2-t1, а Δt0=t'2-t'1 Из этой формулы следует, что длительность одного и того же процесса различна в системах K и K1. В системе K1 длительность процесса больше. Следовательно, он протекает медленнее, чем в системе К. Время, отсчитываемое по часам, которые движутся вместе с телом, называютсобственным временем. Оно самое короткое; наблюдается релятивистский эффект замедления времени (Δ t > Δ to).
. Эту формулу легко получить из преобразований Лоренца, учитывая, что Δt=t2-t1, а Δt0=t'2-t'1 Из этой формулы следует, что длительность одного и того же процесса различна в системах K и K1. В системе K1 длительность процесса больше. Следовательно, он протекает медленнее, чем в системе К. Время, отсчитываемое по часам, которые движутся вместе с телом, называютсобственным временем. Оно самое короткое; наблюдается релятивистский эффект замедления времени (Δ t > Δ to).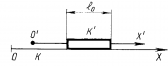
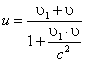
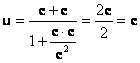 .
.