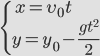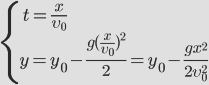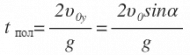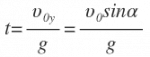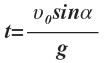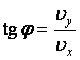|
Движение тела, брошенного горизонтально или под углом к горизонту. |
-
Это движение в плоскости, поэтому для описания движения необходимо 2 координаты.
-
Считаем, что движение происходит вблизи поверхности Земли, поэтому ускорение тела – ускорение свободного падения (a = g).
|
|
|
Так как мы пренебрегаем сопротивлением воздуха, то ускорение направлено только к поверхности Земли (g) – вдоль вертикальной оси (y), вдоль оси х движение равномерное и прямолинейное.
|
|
|
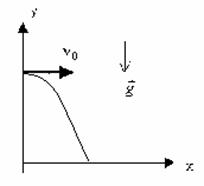
Движение тела, брошенного горизонтально.
|
|
Выразим проекции скорости и координаты через модули векторов.
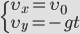
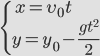
|
 |
|
Для того чтобы получить уравнение траектории, выразим время tиз уравнения координаты x и подставим в уравнение для y:
|
|
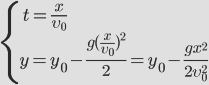 |
- между координатами квадратичная зависимость, траектория – парабола! |
|
Движение тела, брошенного под углом к горизонту.
|
|
Порядок решения задачи аналогичен предыдущей.
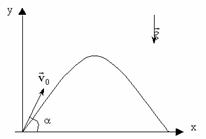
Решим задачу для случая х0=0 и y0=0.
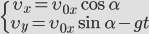

|
 |
|
Докажем, что траекторией движения и в этом случае будет парабола. Для этого выразим координату Y через X (получим уравнение траектории):
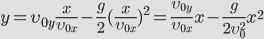 . .
Мы получили квадратичную зависимость между координатами. Значит траектория - парабола. |
|
|
Найдем время полета тела от начальной точки до точки падения. В точке падения координата по вертикальной оси у=0.
|
Время полета:
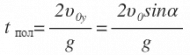
|
|
Следовательно, для решения этой задачи необходимо решить уравнение
|
|
Оно будет иметь решение при t=0 (начало движения) и |
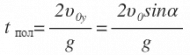 |
|
Зная время полета, найдем максимальное расстояние, которое пролетит тело:
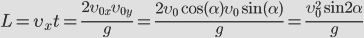
|
Дальность полета:
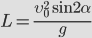
|
|
Из этой формулы следует, что:
- максимальная дальность полета будет наблюдаться при бросании тела (при стрельбе, например) под углом 450;
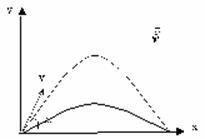
- на одно и то же расстояние можно бросить тело (с одинаковой начальной скоростью) двумя способами – т.н. навесная и настильная баллистические траектории. |
 |
|
Используя то, что парабола – это симметричная кривая, найдем максимальную высоту, которой может достичь тело.
Время, за которое тело долетит до середины, равно: 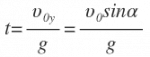
|
Время подъема:
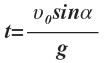
|
|
Тогда: 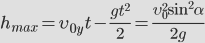
|
Максимальная высота:
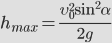
|
|
Скорость тела в любой момент времени направлена по касательной к траектории движения (параболе) и равна 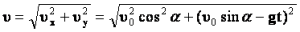
|
|
|
Угол, под которым направлен вектор скорости в любой момент времени:
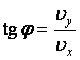
|
|