СИЛА.

Сила – векторная физическая величина, являющаяся мерой взаимодействия тел. Обозначение: .

Существует 4 основных типа взаимодействия: гравитационное, электромагнитное, сильное, слабое.

Все взаимодействия являются проявлениями этих основных типов.

Примеры сил: сила тяжести, сила упругости, вес тела, сила трения, выталкивающая (архимедова) сила, подъемная сила.

Сила характеризуется:

1. Величиной (модулем);

2. Направлением;

3. Точкой приложения.

Из опыта по взаимодействию следует:  или . Величина  характеризует действие второго тела на первое, а величина - характеризует действие первого тела на второе. Т.к. взаимодействие одно и то же, то величину, равную произведению массы тела на ускорение, полученное в данном взаимодействии, можно принять за меру взаимодействия: . Внимание: вектора ускорения и силы всегда сонаправлены!

Т.к. сила – векторная величина, то силы складываются векторно (правила параллелограмма и треугольника). Складывать можно только силы, приложенные к одному телу. Сила, равная векторной сумме всех действующих на тело сил, называетсяравнодействующей: .

Единицы силы:

СИ:  Сила равна одному ньютону, если тело массой 1 кг приобретает ускорение 1м/с².

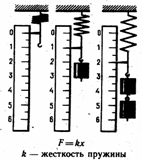
Измерение силы: силы измеряются динамометром по сравнению величины измеряемой силы с силой упругости пружины. Используется линейная зависимость между величиной силы упругости и удлинением пружины.

Для правильного измерения силы необходимо, чтобы при измерении

 тела покоились или двигались прямолинейно и равномерно!

Динамометр градуируется известной силой тяжести.

1-й закон Ньютона.

Роль 1-го закона – он определяет, в каких СО выполняются законы динамики.

Существуют такие системы отсчета, относительно которых тело движется прямолинейно и равномерно или покоится, если на него не действуют другие тела или их действия скомпенсированы.

Другая формулировка: существуют такие системы отсчета, относительно которых тело движется прямолинейно и равномерно или покоится, если равнодействующая всех сил, действующих на тело, равна нулю.

Инерциальные системы отсчета.

СО, в которых выполняется 1-й закон Ньютона, называются инерциальными системами отсчета (ИСО).

Свойство ИСО: все СО, движущиеся прямолинейно и равномерно относительно данной ИСО, тоже являются инерциальными. СО, движущиеся относительно любой ИСО с ускорением, являются неинерциальными

В реальной жизни абсолютной ИСО не существует. СО можно считать инерциальной с той или иной степенью точности в определенных задачах. Например, Землю можно считать ИСО при исследовании движения автомобиля и нельзя – при исследовании полета ракеты (необходимо учитывать вращение).

Принцип относительности Галилея.

Все ИСО – равноправны: законы механики одинаковы во всех ИСО.

Опыт: чем больше сила, тем больше изменение скорости тела (ускорение) - .