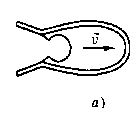
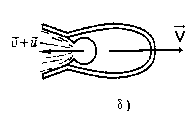
Реактивное движение.

Под реактивным понимают движение тела, возникающее при отделении некоторой его части с определенной скоростью относительно тела. При этом возникает т.н. реактивная сила, сообщающая телу ускорение.

Уравнение Циолковского: Пусть в некоторый момент времени скорость ракеты относительно инерциальной системы, связанной со звездами, равна  (рис. а), а масса ракеты равна М.  Скорость истечения газов относительно выбранной инерциальной системы отсчета равна  , т.к. до начала сгорания топливо имело ту же скорость, что и ракета, а масса топлива m.

Через  малый  интервал  времени  Dt масса ракеты станет равной , где m  - расход топлива (Расходом топлива называется отношение массы сгоревшего топлива ко времени его сгорания). За этот же промежуток времени скорость ракеты изменится на    и станет равной . Тогда получим: 

Раскрыв скобки: 

Слагаемым  можно пренебречь по сравнению с остальными. После приведения подобных членов будем иметь:  или  - уравнение   Мещерского для движения тела переменной массы (1897 г.). Обозначим . Если учесть действие не только реактивной, но и внешней силы, то закон движения для реактивного движения будет выглядеть следующим образом: .

Если представить, что все топливо вытекает одновременно, то согласно закону сохранения импульса:    Mv- mu = 0 или        .   

Здесь m - масса топлива.

Следовательно, скорость движения ракеты тем больше, чем больше скорость истечения топлива и чем большую часть составляет масса топлива от массы ракеты. Поскольку 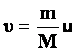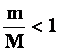, то  v  <  u.