БЕСЕДЫ И МАТЕМАТИЧЕСКИЕ ДОКАЗАТЕЛЬСТВА, КАСАЮЩИЕСЯ ДВУХ НОВЫХ НАУК

День третий 
О естественно-ускоренном движении

Теорема I. Предложение I

Время, в течение которого тело, вышедшее из состояния покоя и движущееся равномерно ускоренно, проходит некоторое расстояние, равно времени, в течение которого это же расстояние было пройдено тем же телом при равномерном движении, скорость которого равняется половине величины наибольшей конечной скорости, достигаемой при первом равномерно ускоренном движении ¹.

Пусть линия АВ представляет время, в течение которого тело, выйдя из состояния покоя в точке С, проходит при равномерно ускоренном движении расстояние CD. Отметим, далее, степени скорости, приобретаемые телом в конце каждой отдельной частицы времени АВ; степени эти, постепенно увеличиваясь, возрастают в конце до величины ЕВ, которую и отложим на линии, перпендикулярной к АВ; соединив точки А и ? и проведя линии, параллельные ЕВ, на равных друг от друга расстояниях, отло женных на АВ, мы представим таким способом возрастающие степени скорости, начиная от А. Разделим линию ЕВ пополам в точке F и проведем линии FG и AG, параллельные АВ и соответ ственно BF. Параллелограмм AGFB будет равен тре угольнику АЕВ, так как линия GF делит АЕ пополам в точке l; если поэтому продолжить параллельные линии, заключенные в треугольнике АЕВ, до IG, то сумма параллельных линий, заключенных в четырехугольнике, будет равна сумме тех же линий, заключенных в треугольнике АЕВ; в самом деле, сумма тех из них, кои заключены в треугольнике IEF, равна сумме заключенных в треугольнике GIA, остающиеся же части, заключенные в трапеции AIFB, являются общими. Так как каждому отдельному времени АВ соответствует и отдельная точка на линии АВ, а проведенные через эти точки парал-лели, заключенные в треугольнике АЕВ, представляют возрастающие степени скорости, в то время как такие же параллели, заключенные внутри параллелограмма, представляют равную им совокупность равномерных скоростей, то ясно, что все моменты скорости ускоренного движения представлены возрастающими параллельными линиями треугольника АЕВ, а равномерного движения - аналогичными линиями параллелограмма GB; то, чего недостает моментам в первое время движения (т. е. моментам, представленным параллельными линиями, заключенными в треугольнике AGI), возмещается моментами, представленными параллельными линиями треугольника IEF. Отсюда следует, что два тела пройдут равные расстояния в одно и то же время, если одно, выйдя из состояния покоя, будет двигаться равномерно ускоренно, а другое просто равномерно со скоростью, равною половине максимальной степени скорости, достигнутой при ускоренном движении, что и требовалось доказать.

Теорема II. Предложение II

Если тело, выйдя из состояния покоя, падает равномерно ускоренно, то расстояния, проходимые им за определенные промежутки времени, относятся между собою, как квадраты времени.

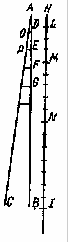Изобразим промежуток времени, начинающийся с какого-либо мгновения А, линией АВ и представим себе, что AD и АЕ суть некоторые части этого промежутка времени. Пусть, далее HI будет линией, вдоль которой падающее тело, вышедшее из состояния покоя, движется равномерно ускоренно, HL - расстояние, пройденное в течение первого промежутка времени AD, и НМ - расстояние, пройденное в промежуток времени АЕ. Утверждаю, что отношение расстояния МН к расстоянию HL равно двойному отношению времени ЕА ко времени AD, другими словами, что отношение расстояний МН, HL равно отношению квадратов ЕА, AD. Проведем линию АС под любым углом к АВ и через точки D и ? последней проведем параллельные линии DO и ЕР, при этом DO будет представлять максимальную степень скорости, приобретенную к мгновению D времени AD, а РЕ - максимальную степень скорости, приобретенную к мгновению ? времени АЕ. Как уже было доказано выше, расстояния, пройденные в одном случае при равномерно ускоренном движении, а в другом при просто равномерном движении, происходящем со скоростью, равной половине максимальной конечной скорости, приобретенной при ускоренном движении, равны между собою. Отсюда ясно, что расстояния МН и LH имеют такую же величину, какую имели бы расстояния, пройденные при равномерном движении со скоростями, равными половинам РЕ и OD, в течение промежутков времени ЕА и DA. Следовательно, если бы можно было доказать, что линии МН и HL относятся между собою, как квадраты ЕА и DA, то было бы доказано и наше предложение. Но в четвертом предложении первой части было указано, что при равномерном движении расстояния находятся в составном отношении скоростей и промежутков времени. В данном случае отношение скоростей равняется отношению промежутков времени (ибо отношение половины РЕ к половине OD или РЕ к OD равно отношению АЕ к AD); следовательно, расстояния относятся как квадраты промежутков времени, что и требовалось доказать.

Следствие I

Из вышеизложенного следует, что если от начального мгновения движения взять равные промежутки времени, как AD, DE, EF, FG, в течение которых телом пройдены расстояния HL, LM, MN, N1, то последние будут относиться между собою как ряд последовательных нечетных чисел, т. е. как 1, 3, 5, 7. Действительно, именно такое отношение существует между разностями квадратов линий произвольной длины, постепенно увеличивающихся на длину наименьшей из этих линий, другими словами, разностями между квадратами всех чисел, начиная с единицы. Таким образом, в то время как скорость возрастает в равные промежутки времени как простой ряд последовательных чисел, расстояния, пройденные за те же промежутки времени, относятся между собой как последовательные нечетные числа.

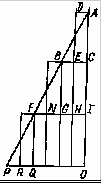Сагредо. Приостановите, пожалуйста, на минуту ваше чтение, так как мне хочется поделиться с вами одной мыслью, пришедшей мне в голову². Для того чтобы лучше изложить ее и сделать более ясной как для самого себя, так и для вас, я сделаю небольшой рисунок. Пусть линия AI изображает промежуток времени, первым мгновением которого является А; через А я провожу прямую линию AF под любым углом к первой, соединяю конечные точки I и F, разделяю время AI пополам в точке С и провожу через нее линию СВ, параллельную IF. Рассматривая СВ как максимальную степень скорости, каковые степени, начиная с мгновения А выхода тела из состояния покоя, идут, возрастая совершенно так же, как линии, параллельные ВС и проведенные в треугольнике ABC (т. е. растут в соответствии с возрастанием времени), я принимаю без дальнейших доказательств, основываясь на предшествующих рассуждениях, что пространство, пройденное телом, падающим с подобной возрастающей скоростью, равно тому пространству, которое оно пройдет, если будет двигаться в продолжение того же времени АС равномерно, и степень его скорости будет равна ЕС, т. е. половине ВС. Пойдем теперь далее и представим себе, что тело, движущееся равномерно ускоренно, достигает точки С и обладает степенью скорости ВС. Ясно

что если бы оно продолжало дальнейшее движение с тою же степенью скорости ВС без ускорения, то в следующий промежуток времени С/ оно прошло бы расстояние, вдвое большее того, которое оно может пройти в равный промежуток времени АС, двигаясь с равномерной скоростью ЕС, равной половине ВС. Так как, однако, тело падает со скоростью, постоянно и равномерно увеличивающейся в равные промежутки времени, то в течение следующего промежутка времени к степени скорости его СВ будут прибавляться наращения, соответствующие параллелям треугольника BFG, равного треугольнику ABC. Таким образом, прибавив к степени скорости G/ половину скорости .FG - наибольшей из приобретенных при ускоренном движении и выражающихся параллелями треугольника BFG,- мы будем иметь степень скорости IN, с которою тело двигалось бы равномерно в течение промежутка времени CI. Так как IN втрое больше ЕС, то выходит, что расстояние, пройденное за второй промежуток времени CI, должно быть. в три раза более того, которое пройдено за первый промежуток времени СА. И если мы представим себе, что к AI прибавляется следующий равный промежуток времени 10, а треугольник возрастает до АРО, то ясно, что если бы движение продолжалось в, течение всего времени 10 со степенью скорости IF, приобретенной при ускоренном движении за время AI, то расстояние, пройденное за время 10, было бы равно учетверенному расстоянию, пройденному в первый промежуток времени АС, так как степень скорости IF в четыре раза превышает ЕС. Но нарастание ускоренного движения идет в треугольнике FPQ совершенно так же, как это имело место в треугольнике ABC, и, приведенное к соответственному равномерному движению, дает приращение, равное ЕС; поэтому, прибавляя QR, равное ЕС, мы получаем общую скорость равномерного движения в течение времени 10, в пять раз превышающую скорость равномерного движения в течение первого периода АС; следовательно, и пройденное пространство будет в пять раз более пройденного в течение первого промежутка времени АС. Таким образом, из этого простого вычисления мы видим, что расстояния, проходимые в равные промежутки времени телом, вышедшим из состояния покоя и движущимся со скоростями, нарастающими в соответствии со временем, относятся между собою как нечетные числа 1, 3, 5 и т. д.; если же мы сложим пройденные пути, то найдем, что в удвоенное время будет пройден путь, в четыре раза больший, в утроенное время - путь, в девять раз больший и т. д.; вообще, пройденные пути будут относиться между собою как квадраты промежутков времени.

Симпличио. Простое и ясное рассуждение синьора Саг-редо понравилось мне, право, много более, нежели несколько неясные для меня доказательства нашего Автора. Теперь я в достаточной мере убежден, что явление должно происходить именно так, если только принять указанное определение равномерно ускоренного движения. Но действительно ли таково ускорение, которым природа пользуется при движении тяжелых падающих тел, остается для меня сомнительным; поэтому для поучения меня и других, мне подобных, не мешало бы теперь привести несколько опытов, из числа многих проделанных, которые показали бы, что различные случаи падения тел совпадают со сделанными заключениями.

Сальвиати. Вы, как подлинный ученый, предъявляете совершенно основательное требование; оно особенно уместно в отношении таких наук, в которых для объяснения законов природы применяются математические доказательства; таковы, например, перспектива, астрономия, механика, музыка и другие аналогичные науки; в них опыт, воспринимаемый чувствами, подтверждает принципы, являющиеся основою для всех дальнейших построений. Однако мне не хотелось бы, чтобы у вас создалось впечатление, будто мы слишком подробно остановились на первом и основном положении, на котором покоится колоссальное здание бесчисленных выводов, лишь в малой доле затронутых нашим Автором в настоящем сочинении; он сделал достаточно уже одним тем, что открыл пытливым умам запертые до сего времени двери. Что касается опытов, то Автор не упустил из виду их произвести, и чтобы убедиться в том, что ускорение естественно падающих тел происходит описанным выше образом, я много раз в обществе нашего Автора производил следующий опыт³. Вдоль узкой стороны линейки или, лучше сказать, деревянной доски длиною около двенадцати локтей⁴, шириною пол-локтя и толщиною около трех дюймов⁵ был прорезан канал шириною немного больше одного дюйма. Канал этот был прорезан совершенно прямым и, чтобы сделать его достаточно гладким и скользким, оклеен внутри возможно ровным и полированным пергаментом; по этому каналу мы заставляли падать гладкий шарик из твердейшей бронзы совершенно правильной формы. Установив изготовленную таким образом доску, мы поднимали конец ее над горизонтальной плоскостью когда на один, когда на два локтя и заставляли скользить шарик по каналу (описанному выше), отмечая способом, о котором речь будет идти ниже, время, необходимое для пробега им всего пути; повторяя много раз один и тот же опыт, чтобы точно определить время, мы не находили никакой разницы даже на одну десятую времени биения пульса. Точно установив это обстоятельство, мы заставляли шарик проходить лишь четвертую часть длины того же канала; измерив время его падения, мы всегда находили самым точным образом, что оно равняется всего половине того, которое наблюдалось в первом случае. Производя далее опыты при различной иной длине пути, сравнивая время прохождения всей линейки со временем прохождения половины, двух третей, трех четвертей или любых иных частей ее и повторяя опыты сотни раз, мы постоянно находили, что отношение пройденных путей равно отношению квадратов времени их прохождения при всех наклонах плоскости, т. е. канала, по которому скользил шарик. При этом мы наблюдали также, что промежутки времени пробега пути при различных наклонах относятся между собою именно так, как утверждает и доказывает далее Автор. Что касается способа измерения времени, то мы пользовались большим ведром, наполненным водою и подвешенным наверху; в дне ведра был проделан узкий канал; через этот последний вода изливалась тонкой струйкой и собиралась в маленьком бокале в течение всего того времени, как шарик спускался по всему каналу или части его; собранные таким образом количества воды каждый раз взвешивались на точнейших весах; разность и отношение веса воды для разных случаев давали нам разность и отношение времен падения, и притом с такою точностью, что, как я уже упоминал, повторяя один опыт много и много раз, мы не могли заметить сколько-нибудь значительных отклонений. <...>

* Г. Галилей Избранные труды в двух томах, т. 2 M , 1964, с 248-254 
¹Данная теорема и ее доказательство были известны уже в XIV в , она часто встречалась в печатных трудах XVI в. 
²Далее Галилей обобщает полученные соотношения для свободного падения на все случаи равномерно ускоренного движения. 
³ Далее Галилей описывает свои замечательные опыты по нахождению закона равноускоренного движения. 
⁴ 1 локоть-древняя мера длины, соответствующая длине локтевой кости человека, размер которой колебался от 40 до 64 см. 
⁵ 1 дюйм=1/12 фута=0,0254 м.