Из статьи А. Эйнштейна

"К электродинамике движущихся тел"

Известно, что электродинамика Максвелла в современном виде приводит в применении к движущимся телам к асимметрии, которая несвойственна, по-видимому, самим явлениям. Вспомним, например, электродинамическое взаимодействие между магнитом и проводником с током. Наблюдаемое явление зависит здесь только от относительного движения проводника и магнита, в то время как, согласно обычному представлению, два случая, в которых движется либо одно, либо другое из этих тел, должны быть строго разграничены. В самом деле, если движется магнит, а проводник покоится, то вокруг магнита возникает электрическое поле, обладающее некоторым количеством энергии, которое в тех местах, где находятся части проводника, порождает ток. Если же магнит находится в покое, а движется проводник, то вокруг магнита не возникает никакого электрического поля, зато в проводнике возникает электродвижущая сила, которой самой по себе не соответствует никакая энергия, но которая - при предполагаемой тождественности относительного движения в обоих интересующих нас случаях - вызывает электрические токи той же величины и того же направления, что и электрическое поле в первом случае. Примеры подобного рода, как и неудавшиеся попытки обнаружить движение Земли относительно "светоносной среды", ведут к предположению, что не только в механике, но и в электродинамике никакие свойства явлений не соответствуют понятию абсолютного покоя и даже, более того, к предположению, что для всех координатных систем, для которых справедливы уравнения механики, справедливы те же самые электродинамические и оптические законы... Это предположение (содержание которого в дальнейшем будет называться "принципом относительности") мы намерены превратить в предпосылку и сделать, кроме того, добавочное допущение, находящееся с первым лишь в кажущемся противоречии, а именно, что свет в пустоте всегда распространяется с определенной скоростью V, не зависящей от состояния движения излучающего тела. Эти две предпосылки достаточны для того, чтобы, положив в основу теорию Максвелла для покоящихся тел, построить простую, свободную от противоречий электродинамику движущихся тел. Введение "светоносного эфира" оказывается при этом излишним, поскольку в предлагаемой теории не вводится "абсолютно покоящееся пространство", наделенное особыми свойствами, а также ни одной точке пустого пространства, в котором протекают электромагнитные процессы, не приписывается какой-нибудь вектор скорости.
Развиваемая теория основывается, как и всякая другая электродинамика, на кинематике твердого тела, так как суждения всякой теории касаются соотношений между твердыми телами (координатными системами), часами и электромагнитными процессами. Недостаточное понимание этого обстоятельства является корнем тех трудностей, преодолевать которые приходится теперь электродинамике движущихся тел...

Определение одновременности

Пусть имеется координатная система, в которой справедливы уравнения механики Ньютона. Для отличия от вводимых позже координатных систем и для уточнения терминологии назовем эту координатную систему "покоящейся системой".
Если некоторая материальная точка находится в покое относительно этой координатной системы, то ее положение относительно последней может быть определено методами эвклидовой геометрии с помощью твердых масштабов и выражено в декартовых координатах.
Желая описать движение какой-нибудь материальной точки, мы задаем значения ее координат как функций времени. При этом следует иметь в виду, что подобное математическое описание имеет физический смысл только тогда, когда предварительно выяснено, что подразумевается здесь под "временем". Мы должны обратить внимание на то, что все наши суждения, в которых время играет какую-либо роль, всегда являются суждениями об одновременных событиях. Если я, например, говорю: "Этот поезд прибывает сюда в 7 часов",- то это означает примерно следующее: "Указание маленькой стрелки моих часов на 7 часов и прибытие поезда суть одновременные события". [Здесь не будет обсуждаться неточность, содержащаяся в понятии одновременности двух событий, происходящих (приблизительно) в одном и том же месте, которая должна быть преодолена также с помощью некоторой абстракции - Прим авт.]
Может показаться, что все трудности, касающиеся определения "времени", могут быть преодолены тем, что вместо слова "время", я напишу "положение маленькой стрелки моих часов". Такое определение действительно достаточно в случае, когда речь идет о том, чтобы определить время лишь для того самого места, в котором как раз находятся часы; однако это определение уже недостаточно, как только речь будет идти о том, чтобы связать друг с другом во времени ряды событий, протекающих в различных местах, или, что сводится к тому же установить время для тех событий, которые происходят в местах, удаленных от часов.
Желая определить время событий, мы смогли бы, конечно, удовлетвориться тем, что заставили бы некоторого наблюдателя, находящегося с часами в начале координат, сопоставлять соответствующее положение стрелки часов с каждым световым сигналом, идущим к нему через пустоту и дающим знать о регистрируемом событии. Такое сопоставление связано, однако, с тем неудобством, известным нам из опыта, что оно не будет независимым от местонахождения наблюдателя, снабженного часами. Мы придем к гораздо более практическому определению путем следующих рассуждений.
Если в точке А пространства помещены часы, то наблюдатель, находящийся в А, может устанавливать время событий в непосредственной близости от А путем наблюдения одновременных с этими событиями положений стрелок часов. Если в другой точке В пространства также имеются часы (мы добавим: "точно такие же часы, как в точке А"), то в непосредственной близости от В тоже возможна временная оценка событий находящимся в В наблюдателем. Однако невозможно без дальнейших предположений сравнивать во времени какое-либо событие в А с событием в В; мы определили пока только "А-время" и "В-время", но не общие для А и В "время". Последнее можно установить, вводя определение, что "время", необходимое для прохождения света из А в В, равно "времени", требуемому для прохождения света из В в А. Пусть в момент tА по "А-времени" луч света выходит из А в В, отражается в момент tВ по "В-времени" от В к А и возвращается назад в А момент tА по "А-времени". Часы в А и В будут идти, согласно определению, синхронно, если
tВ-tА = t'А -t'В.
Мы сделаем допущение, что это определение синхронности можно дать непротиворечивым образом и притом для сколь угодно многих точек и что, таким образом, справедливы следующие утверждения:
1) если часы в В идут синхронно с часами в А, то часы в А идут синхронно с часами в В;
2) если часы в А идут синхронно как с часами в В, так и с часами в С, то часы В и С также идут синхронно относительно друг друга.
Таким образом, пользуясь некоторыми (мысленными) физическими экспериментами, мы установили, что нужно понимать под синхронно идущими, находящимися в различных местах покоящимися часами, и благодаря этому, очевидно, достигли определения понятий: "одновременность" и "время". "Время" события - это одновременное с событием показание покоящихся часов, которые находятся в месте события и которые идут синхронно с некоторыми определенными покоящимися часами, причем с одними и теми же часами при всех определениях времени.
Согласно опыту, мы положим также, что величина

есть универсальная константа (скорость света в пустоте).
Существенным является то, что мы определили время с помощью покоящихся часов в покоящейся системе; будем называть это время, принадлежащее к покоящейся системе, "временем покоящейся системы".

Об относительности длин и промежутков времени

Дальнейшие соображения опираются на принцип относительности и на принцип постоянства скорости света. Мы формулируем оба принципа следующим образом.
1. Законы, по которым изменяются состояния физических систем, не зависят от того, к которой из двух координатных систем, движущихся относительно друг друга равномерно и прямолинейно, эти изменения состояния относятся.
2. Каждый луч света движется в "покоящейся" системе координат с определенной скоростью V, независимо от того, испускается ли этот луч света покоящимся или движущимся телом.
При этом ,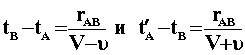
причем "промежуток времени" следует понимать в смысле определения... [приведенного выше].
Пусть нам дан покоящийся твердый стержень, и пусть длина его, измеренная также покоящимся масштабом, есть l. Теперь представим себе, что стержню, ось которого направлена по оси X покоящейся координатной системы, сообщается равномерное и параллельное оси X поступательное движение (со скоростью v) в сторону возрастающих значений х. Поставим теперь вопрос о длине движущегося стержня, которую мы полагаем определенной с помощью следующих двух операций:
а) наблюдатель движется вместе с указанным масштабом и с измеряемым стержнем и измеряет длину стержня непосредственно путем прикладывания масштаба так же, как если бы измеряемый стержень, наблюдатель и масштаб находились в покое;
б) наблюдатель устанавливает с помощью расставленных в покоящейся системе синхронных… покоящихся часов, в каких точках покоящейся системы находится начало и конец измеряемого стержня в определенный момент времени t. Раccтояние между этими двумя точками, измеренное использованным выше, но уже покоящимся масштабом, есть длина, которую можно обозначить как "длину стержня".
Согласно принципу относительности, длина, определяемая Операцией "а", которую мы будем называть "длиной стержня движущейся системе", должна равняться длине покоящегося стержня.
Длину, устанавливаемую операцией "б", которую мы будем называть "длиной (движущегося) стержня в покоящейся системе", мы определим, основываясь на наших двух принципах, и найдем, что она отлична от l.
В обычно применяемой кинематике принимается без оговорок, что длины, определенные посредством двух упомянутых операций, равны друг другу, или, иными словами, что движущееся твердое тело в момент времени t в геометрическом отношении вполне может быть заменено тем же телом, когда оно покоится в определенном положении.
Представим себе, что к обоим концам стержня (А и В) прикреплены часы, которые синхронны с часами покоящейся системы, т. е. показания их соответствуют "времени покоящейся системы" в тех местах, в которых эти часы как раз находятся; следовательно, это часы "синхронны в покоящейся системе".
Представим себе далее, что у каждых часов находится движущийся с ними наблюдатель и что эти наблюдатели применяют к обоим часам... критерий синхронности хода двух часов. Пусть в момент времени tА из А выходит луч света" отражается в В в момент времени t B и возвращается назад в А в момент времени t'А . Принимая во внимание принцип постоянства скорости света, находим:

,

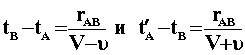где rАB - длина движущегося стержня, измеренная в покоящейся системе. Итак, наблюдатели, движущиеся вместе со стержнем, найдут, что часы в точках А и В не идут синхронно, в то время как наблюдатели, находящиеся в покоящейся системе, объявили бы эти часы синхронными.
Итак, мы видим, что не следует придавать абсолютного значения понятию одновременности. Два события, одновременные при наблюдении из одной координатной системы, уже не воспринимаются как одновременные при рассмотрении из системы, движущейся относительно данной системы.

Из статьи А. Эйнштейна
"Теория относительности"

Перечислим кратко отдельные результаты, полученные до настоящего времени благодаря теории относительности. Она дает простую теорию принципа Доплера, аберрации... Она говорит о справедливости уравнений поля Максвелла - Лоренца и для электродинамики движущихся тел. Законы отклонения быстрых катодных лучей и одинаковых с ними по природе a-лучей радиоактивных веществ, вообще законы движения быстро движущихся материальных частиц выводятся с помощью теории относительности без привлечения особых дополнительных гипотез.
Однако важнейший результат, достигнутый пока теорией относительности, - это вывод соотношения между инертной массой физической системы и содержанием энергии в ней. Пусть тело обладает в некотором определенном состоянии инертной массой М. Если этому телу сообщается каким-то образом энергия Е, то, согласно теории относительности, его инертная масса возрастает вследствие этого до значения , где с - скорость света в пустоте. Поэтому закон сохранения массы, считавшийся до сих пор справедливым, видоизменяется и объединяется в один закон с законом сохранения энергии. Этот результат говорит о том, что инертную массу М тела следует понимать как содержание энергии Мс². Прямого экспериментального подтверждения этого важного результата у нас пока нет, однако мы знаем частные случаи, для которых справедливость "закона инерции энергии" можно доказать, не прибегая к теории относительности..,

Общая теория относительности

Специальная теория относительности основана на идее, что определенные системы координат (инерциальные системы) являются равноправными для формулировки законов природы; к таким системам координат принадлежат те, в которых выполняется закон инерции и закон постоянства скорости света в пустоте. Но являются ли эти системы координат на самом деле выделенными в природе, или же эта привилегированность возникает вследствие несовершенного понимания законов природы? Конечно, закон Галилея на первый взгляд выделяет инерциальные системы из всех других движущихся систем координат. Но закон инерции обладает недостатком, который обесценивает этот аргумент.
...Представим себе часть пространства, свободную от действия сил в смысле классической механики, иными словами, достаточно удаленную от тяготеющих масс. Тогда в соответствии с механикой существует инерциальная система К, относительно которой масса М, предоставленная самой себе в рассматриваемой части пространства, движется прямолинейно и равномерно. Если теперь ввести систему координат К', равномерно ускоренную относительно системы К, то по отношению к системе К' масса М, предоставленная самой себе, будет двигаться не по прямой, а по параболе, подобно тому, как движется масса вблизи поверхности Земли под действием силы тяжести. Можно ли отсюда заключить, что система К' (абсолютно) ускорена? Это заключение было бы неправомерным. Систему К' можно с таким же правом считать "покоящейся", предполагая лишь, что в системе К' существует однородное гравитационное поле, являющееся причиной ускоренного движения тел относительно К'.
Против такого утверждения можно было бы возразить, что не указаны массы, порождающие это гравитационное поле. Однако их можно считать бесконечно удаленными, не вступая противоречие с основами механики Ньютона. Кроме того, мы не знаем, с какой точностью соответствует действительности закон тяготения Ньютона.
Одно обстоятельство говорит в пользу нашего утверждения. Относительно системы К' все массы, независимо от их конкретных физических и химических свойств, падают с одинаковым ускорением. Опыт показывает, что это справедливо и для гравитационного поля, причем с необычайной точностью. Примечательный факт, что мы знаем гравитационное поле как состояние пространства, в котором поведение тел такое же, как и в системе К', делает совершенно естественной гипотезу о том, что в системе К' существует гравитационное поле, по существу тождественное полям тяготения, порождаемым массами в соответствии с законом Ньютона.
При этом способе рассмотрения не существует никакого реального разделения на инерцию и гравитацию, поскольку ответ на вопрос о том, находится ли тело в определенный момент исключительно под действием инерции или под комбинированным воздействием инерции и гравитации, зависит от системы координат, т. е. от способа рассмотрения...
Простое рассуждение показывает, что путь луча света, распространяющегося в инерциальной системе К прямолинейно и равномерно, в системе координат К', совершающей ускоренное поступательное движение, будет криволинейным. Отсюда мы заключаем, что лучи света искривляются гравитационным полем... Это следствие впервые было подтверждено во время Солнечного затмения 1919 г. ...
Далее, исходя из лоренцева сокращения, которое выше но получено как следствие специальной теории относительности, можно сделать вывод о том, что расположение практически жестких тел в системе К описывается геометрией Евклида неточно и что скорость хода одинаково устроенных часов является функцией точки. Другими словами, в общей теории относительности не существует геометрии и кинематики, не зависящих от физических процессов, так как свойства масштабов и часов определяются гравитационным полем.
В разительном контрасте с глубоким изменением, внесенным общей теорией относительности в основы физики, находится ничтожное различие между количественными предсказаниями новой и старой теорий. Кроме уже упомянутого искривления лучей света в гравитационном поле Солнца, обнаруживаемого только при полном солнечном затмении, следует назвать еще медленное вращение эллиптической орбиты планеты Меркурий (40 с за 100 лет), которое нашло объяснение в общей теории относительности, но не могло быть объяснено в теории тяготения Ньютона. Наконец, общая теория относительности предсказывает незначительный сдвиг спектральных линий света, испускаемого атомами на поверхности Солнца или неподвижных звезд, по сравнению со спектральными линиями света, испускаемого на поверхности Земли. Наблюдениями установлено, что существование этого эффекта является весьма вероятным, но пока еще не вполне достоверным.