О некоторых ошибках в школьных учебниках

Казакевич Н.А.,

учитель физики ЧОУ «Школа «ЛИДЕР»,
эксперт ЕГЭ по физике;
e-mail: abelevna@mail.ru

Не секрет, что в школьных учебниках встречаются ошибки, причем не только ошибки-опечатки и стилистические, являющиеся следствием недоработок корректоров и редакторов, но и принципиальные. В этой статье я хочу обратить внимание авторов учебников, а также редакторов-корректоров соответствующих издательств на две кочующие из учебника в учебник математики, физики, химии и т.д. ошибки, которые почему-то пропускают редакторы и корректоры, и на некоторые принципиальные ошибки.
Первая из этих ошибок могла бы быть предотвращена редактором-корректором, и почему этого не происходит, мне непонятно. Встречается она почти всегда, когда речь идет о результате умножения с указанием сомножителей (правда, теперь почему-то слово «сомножители» употреблять не принято, говорят о множителях, видимо, с целью подчеркнуть их равноправие для объектов, на которые распространяется коммутативный закон умножения). Для примера рассмотрим словесную формулировку для одной из формул сокращенного умножения: «Квадрат суммы двух чисел равен квадрату первого числа плюс удвоенное произведение первого на второе плюс квадрат второго числа». Но произведение (как результат умножения) может быть только одного числа и другого. Когда говорят о произведении чего-то на что-то, переносят управление в словосочетаниях со словом «умножение» (в этом случае как раз верно говорить об умножении одного числа на другое) на словосочетания со словом «произведение», и это, безусловно, ошибка.

Вторая ошибка связана с неправильным пониманием некоторыми авторами и редакторами-корректорами смысла термина «процент». По определению процент – это способ выражения безразмерных величин, процент показывает, какую часть одно значение величины составляет от другого, математически записывается так: 0,01 = 1%. Таким образом, единицей измерения процент не является! Тем не менее, даже в типографике процент называют единицей измерения и требуют отбивания пробелом численного значения и знака процента наравне с метрами, вольтами, молями и т.п. В формулах-определениях многих величин в учебниках запись выглядит так:

коэффициент полезного действия
относительная влажность воздуха:		и
массовая доля растворенного вещества в растворе:

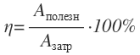
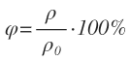
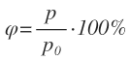
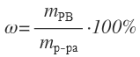
и т.п.
Те, кто включил такие записи в учебники, не понимают, что в пояснении к формулам

;

;

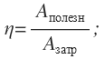
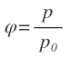
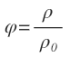
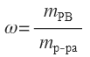
вполне достаточно написать, что соответствующие величины принято выражать в процентах. И тогда ученик, рассчитав, например, значение влажности воздуха, совершенно спокойно напишет: φ=0,6=60%. В конце концов, в случае обратного перевода из процентов в доли единицы (а расчеты по большей части проводятся в долях единицы, а не в процентах) включать в формулу деление на 100% никому пока в голову не пришло!

Замечу, кстати, что и для величин «с наименованием» никто не пишет, если, например, нужно выразить ответ в сантиметрах, а расчеты проводились в метрах:
(подразумевая, что		).

  
Еще одна ошибка, по непонятным причинам возникшая, содержится в разных учебниках физики в определении понятия «гармонические колебания».
Возьмем учебник физики для профильной школы: Мякишев Г.Я., Синяков А.З. Физика: Колебания и волны. 11 кл.: Учеб. для углубленного изучения физики. – М.: Дрофа, 2010. – С. 15: «Периодические изменения физической величины в зависимости от времени по закону синуса или косинуса называются гармоническими колебаниями». Не будь этот учебник адресован одиннадцатиклассникам – вполне уже взрослым людям, стоящим на пороге школы, да еще изучающим физику углубленно – я бы списала этот самый «закон синуса или косинуса» на попытку подстроиться под плохо подготовленных к восприятию научного языка учеников. Но это не тот случай. Ну нет закона синуса и косинуса. Нигде нет – ни в физике, ни в математике. Есть периодические функции, которые необходимо использовать для описания периодических процессов, не более – но и не менее того. Почему нельзя сформулировать определение, например, так: «Гармонические колебания – колебания, при которых зависимость от времени физических величин, описывающих процесс, выражается функцией синус или косинус»? А то ведь и равноускоренное движение можно определить так: «Это движение, при котором координата и перемещение в зависимости от времени изменяются по квадратичному закону»…

Ну, кстати, если уж придираться по полной программе, то в определении гармонических колебаний, приведенном в учебнике Мякишева, есть еще одна ошибка. Гармонические колебания – это явление. Зависимость от времени физических величин, характеризующих процесс, – это описание явления. Нельзя отождествлять процесс с его описанием. Нельзя, например, говорить: «Измерение тока в электрической цепи». Ток – это явление, суть которого – упорядоченное движение заряженных частиц в проводнике. Одна из физических величин, с помощью которой описывают протекание тока, называется силой тока, именно ее измеряют с помощью амперметра.
Следующая ошибка, на которую хочется обратить внимание, – скорее авторская, чем редакторская, она связана с использованием некорректного когда-то «изобретенного» методистами термина «равнозамедленное движение» (иногда еще используется термин «равнопеременное движение», что вообще не выдерживает никакой критики).
При равноускоренном движении в зависимости от направления вектора ускорения относительно направления вектора скорости модуль скорости может либо возрастать, либо убывать. Есть физическая величина «ускорение», характеризующая быстроту изменения скорости. При равноускоренном движении вектор ускорения не изменяется ни по модулю, ни по направлению: . Движение при этом может происходить как с возрастанием модуля скорости, так и с убыванием. Возрастает или убывает модуль скорости, зависит исключительно от того, как ориентированы относительно друг друга вектор скорости и ускорения. Траектория может быть как прямолинейной, так и криволинейной (параболической), форма траектории определяется углом между начальной скоростью и ускорением. Если движение прямолинейное, модуль скорости возрастает, когда векторы скорости и ускорения сонаправлены, и убывает, если эти векторы противонаправлены; если траектория криволинейная (например, при движении тела, брошенного под углом к горизонту), модуль скорости будет убывать, если угол между векторами скорости и ускорения тупой, и возрастать, если острый (иначе – модуль скорости возрастает, если проекция вектора скорости на направление ускорения положительна, и убывает, если отрицательна).
Желание подчеркнуть, что движение происходит с убыванием модуля скорости, называя его «равнозамедленным движением», связано с тем, что в повседневной жизни под ускорением процессов понимают увеличение интенсивности их протекания, а если интенсивность падает с течением времени, говорят о замедлении (рост инфляции замедлился, рост экономики замедлился и т.п.). Однако в механике есть физическая величина «ускорение», от названия которой и происходит четко определенный по смыслу термин «равноускоренное движение», перенос бытового понимания слова «ускорение» на этот термин неправильно – ведь никакой физической величины «замедление» не существует.
Четкость мышления у учащихся формируется, в частности, четкостью формулировок понятий в школьных учебниках. Хотелось бы, чтобы неточностей и ошибок в учебной литературе было как можно меньше.